Resampling

Tidy Data Science with the Tidyverse and Tidymodels

W. Jake Thompson

https://tidyds-2021.wjakethompson.com · https://bit.ly/tidyds-2021

Tidy Data Science with the Tidyverse and Tidymodels is licensed under a Creative Commons Attribution 4.0 International License.

Your Turn 0Open the R Notebook materials/exercises/10-resampling.Rmd
Run the setup chunk


01:00

Hypothesis

As the number of 🦄 increases, so does the number of 🌈.

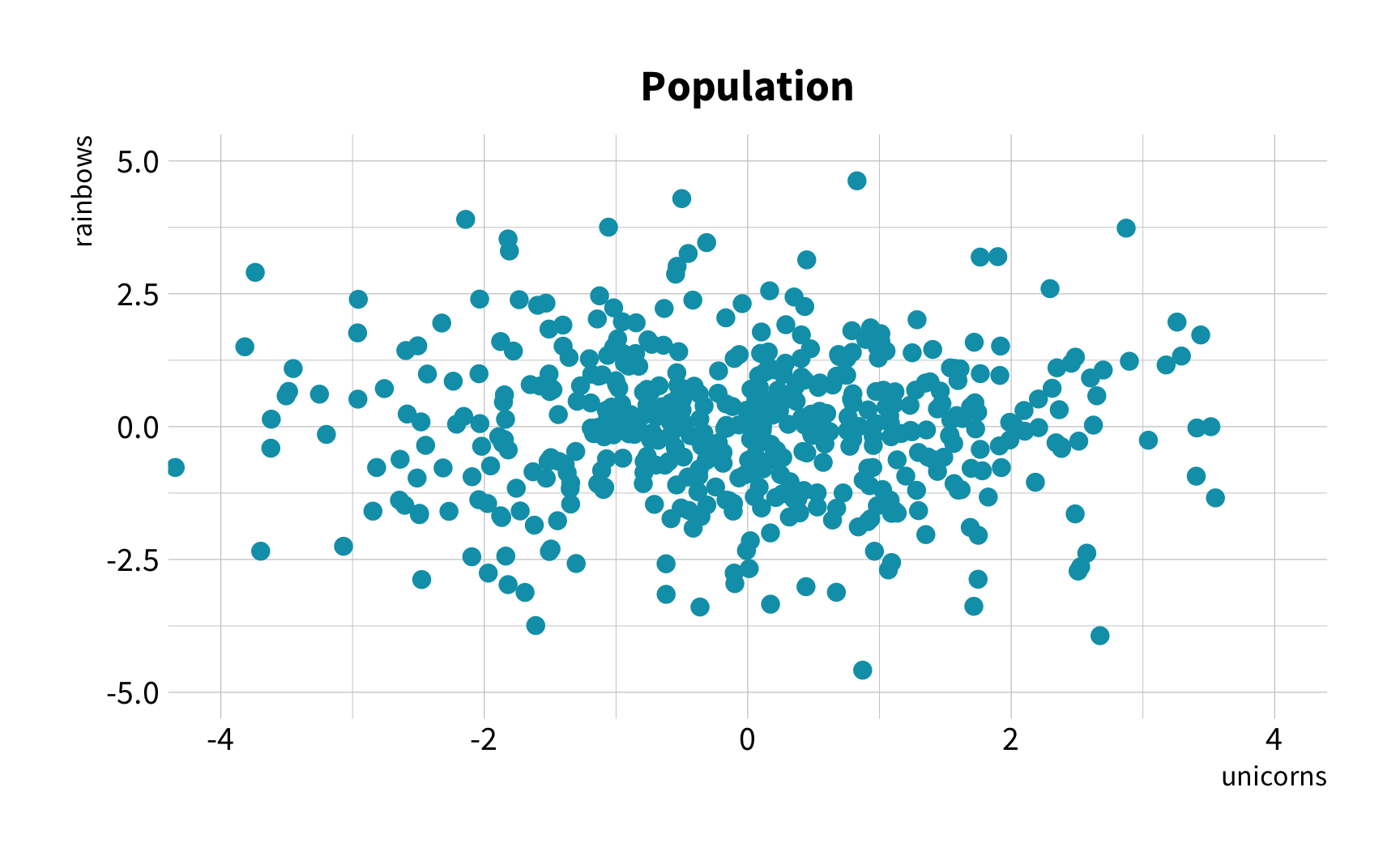
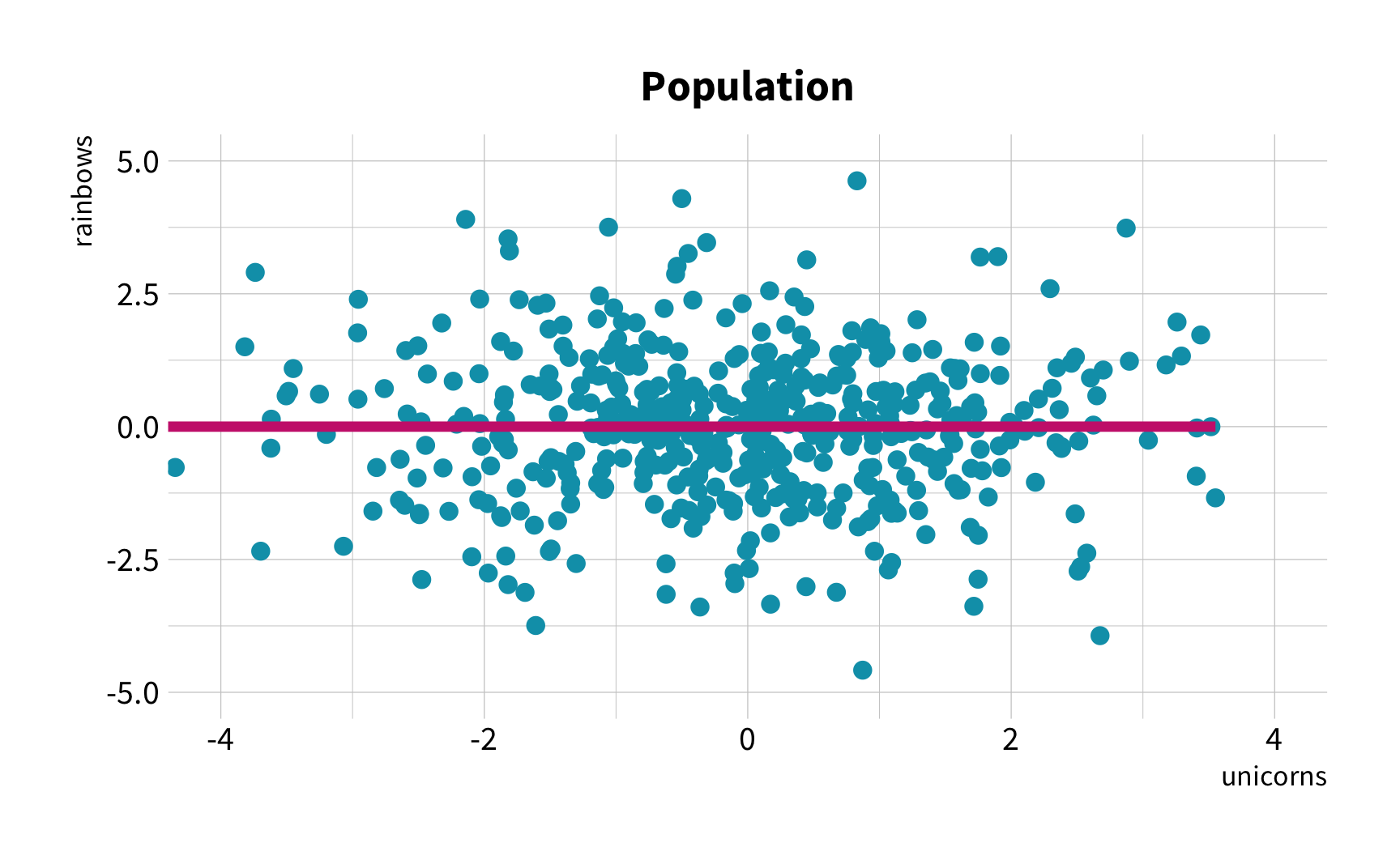
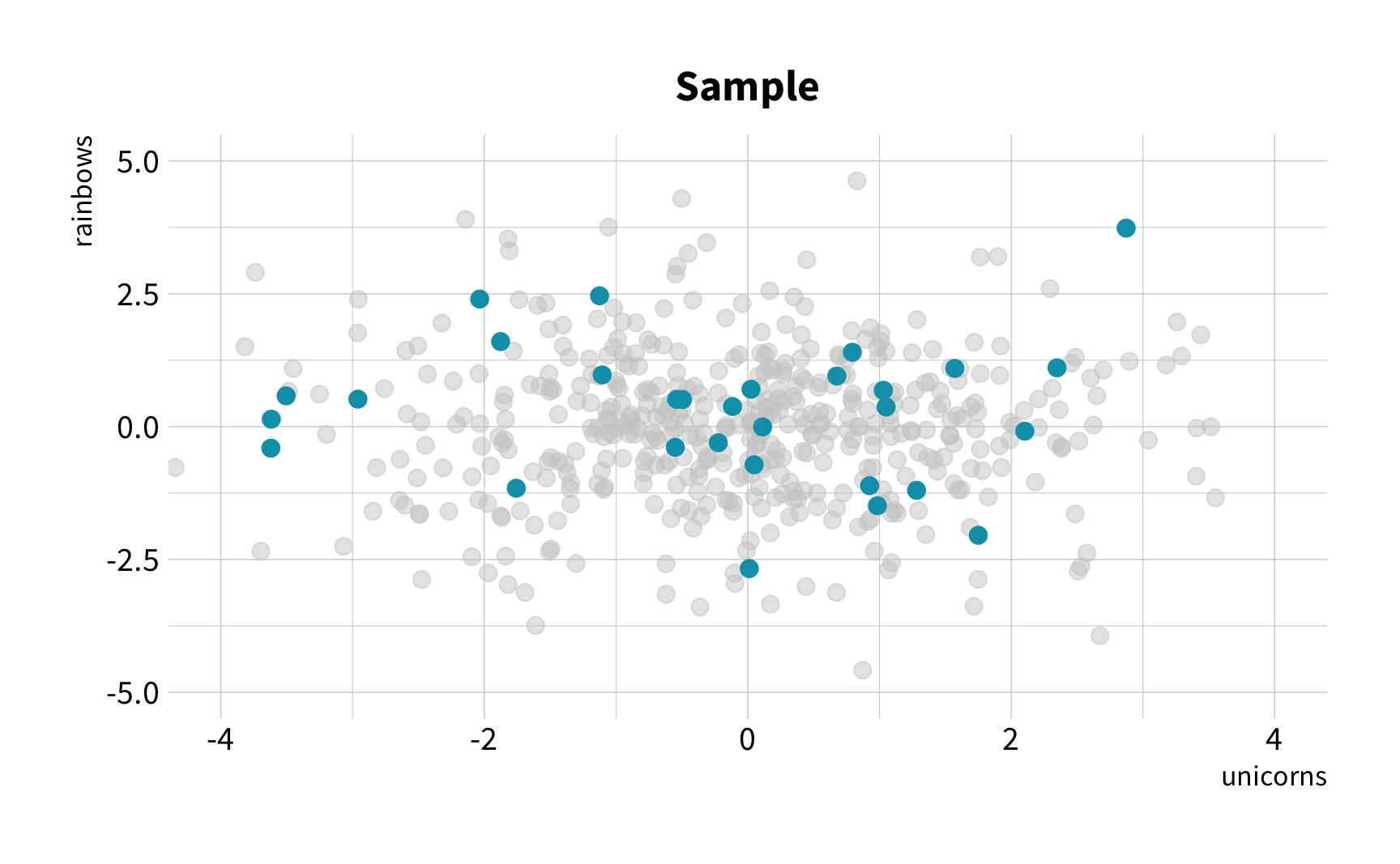
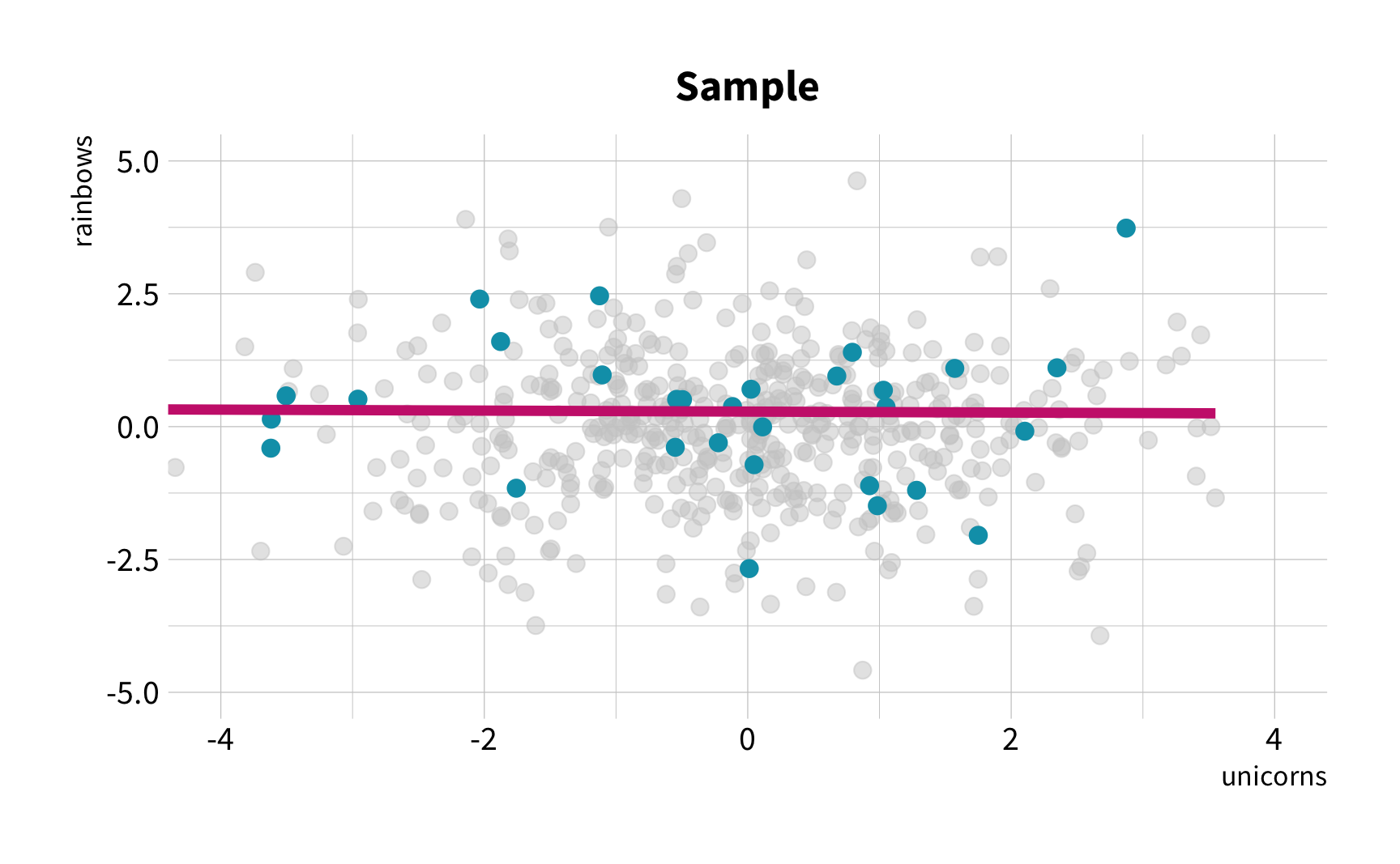
The Challenge

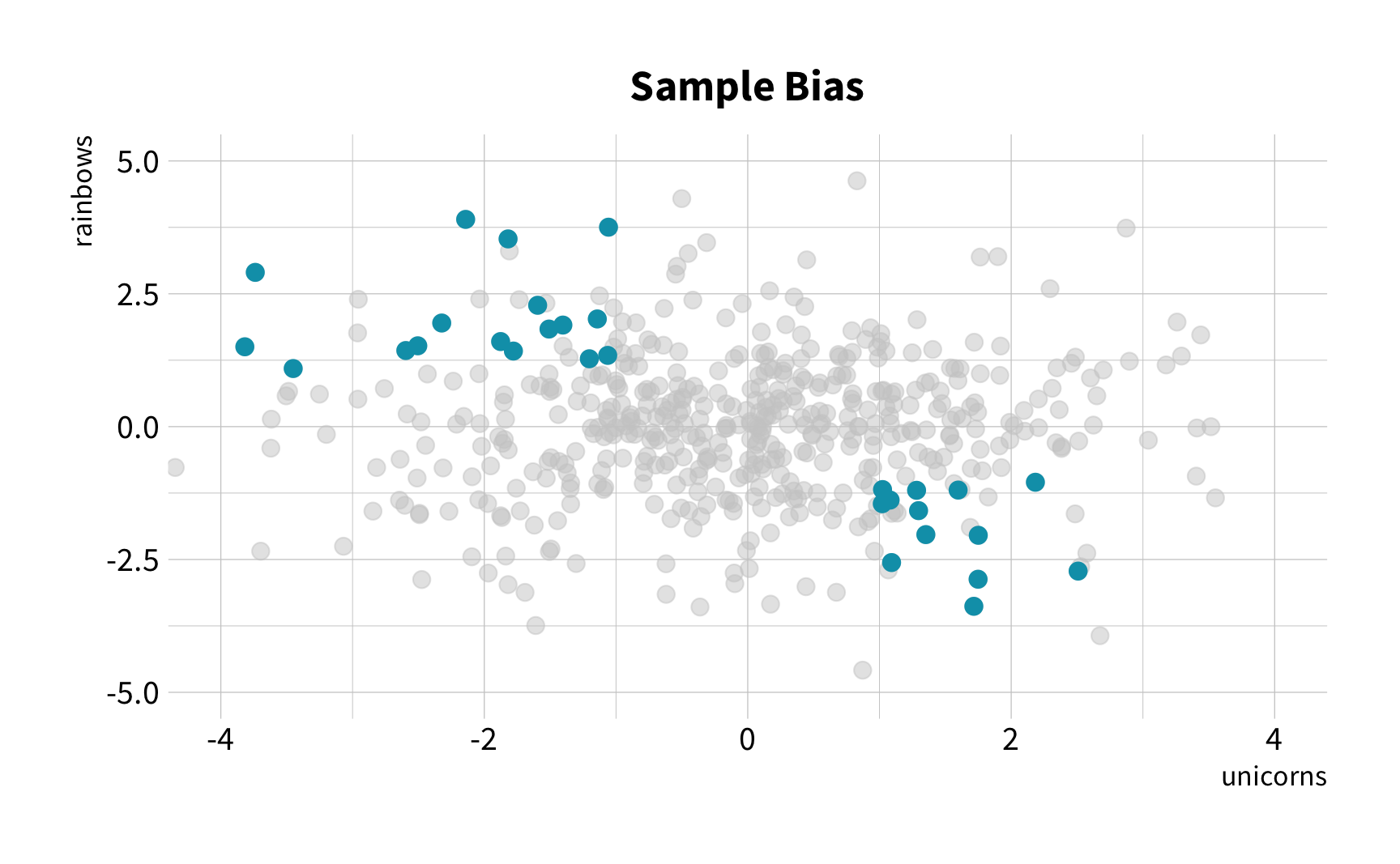
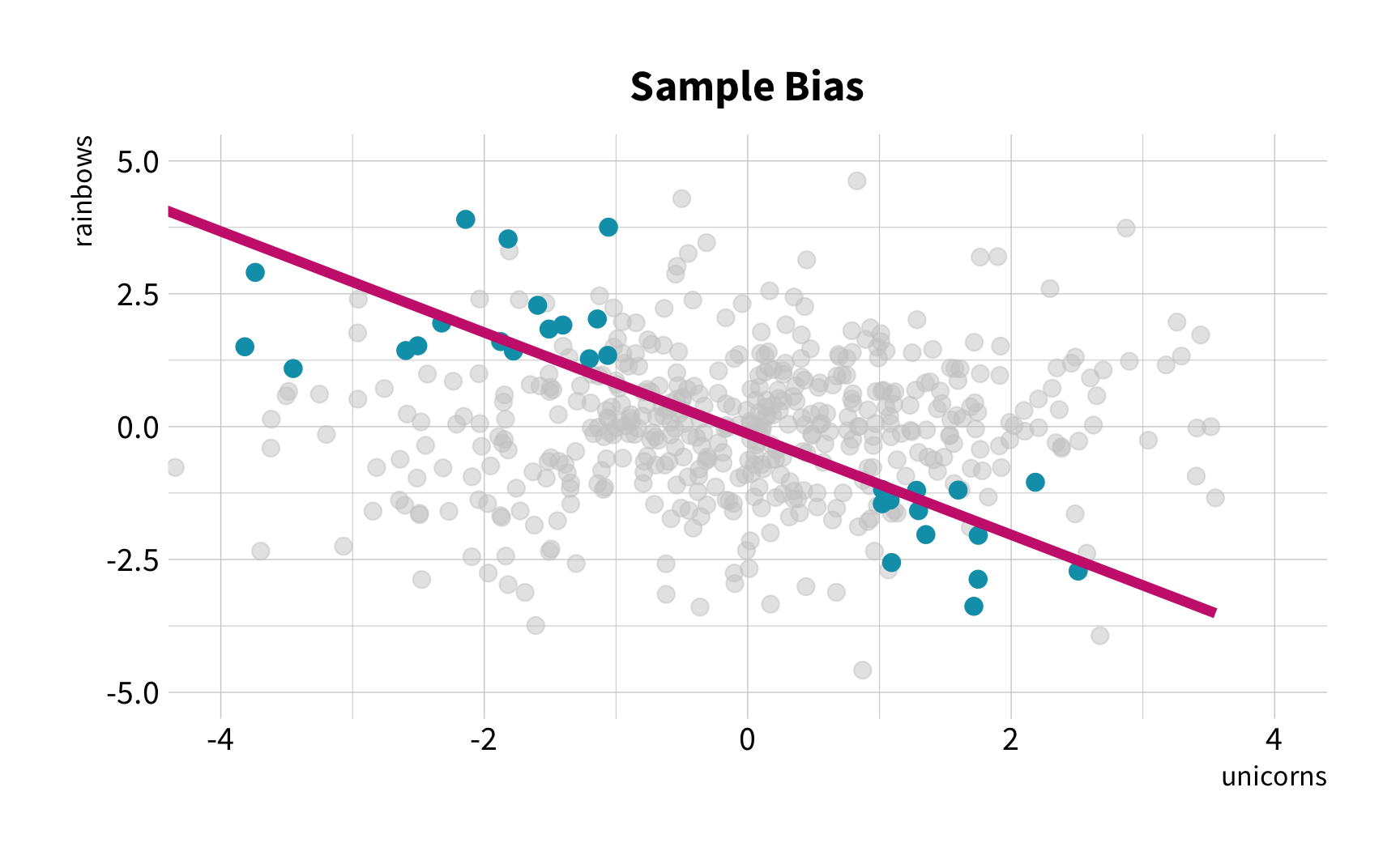
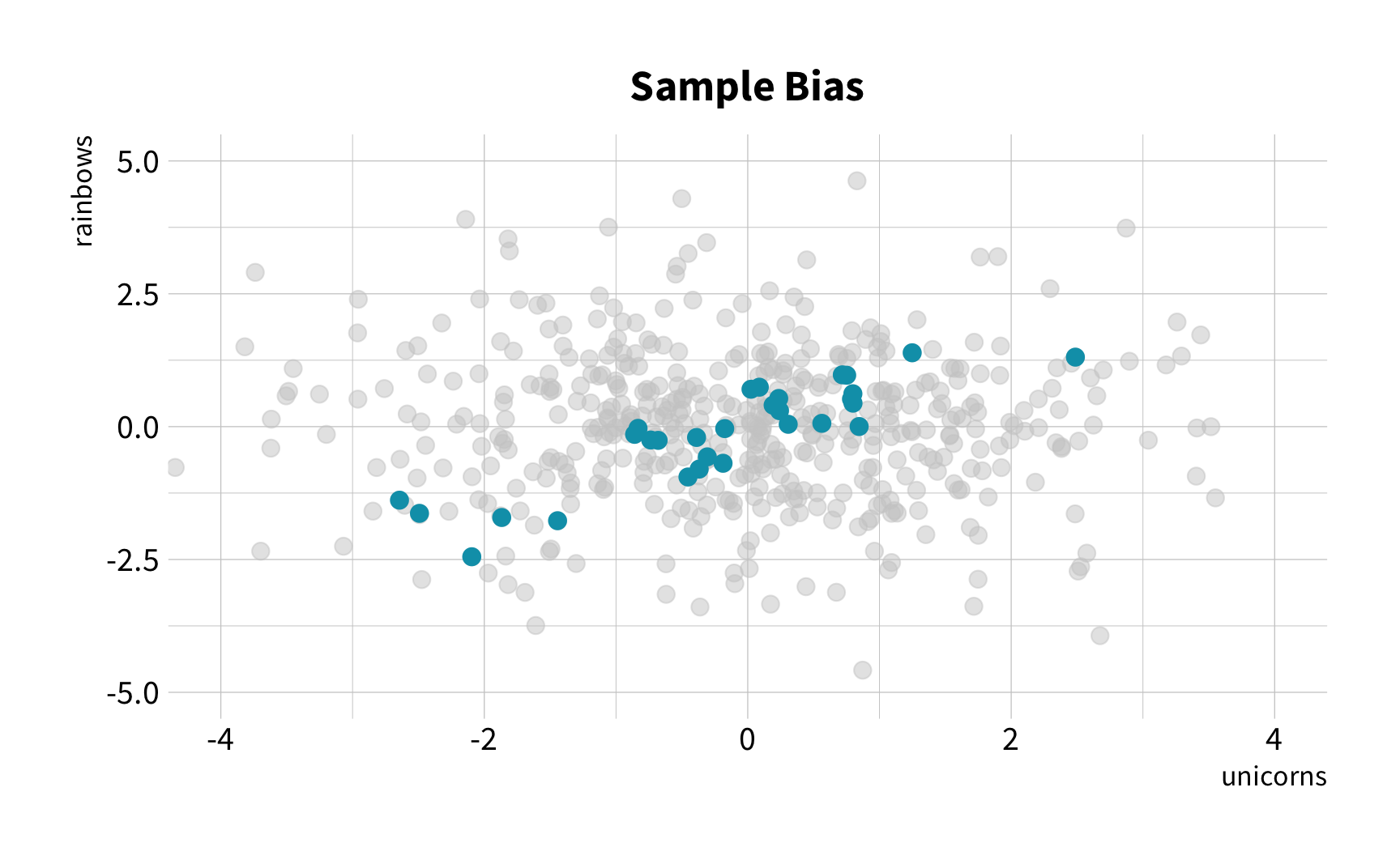
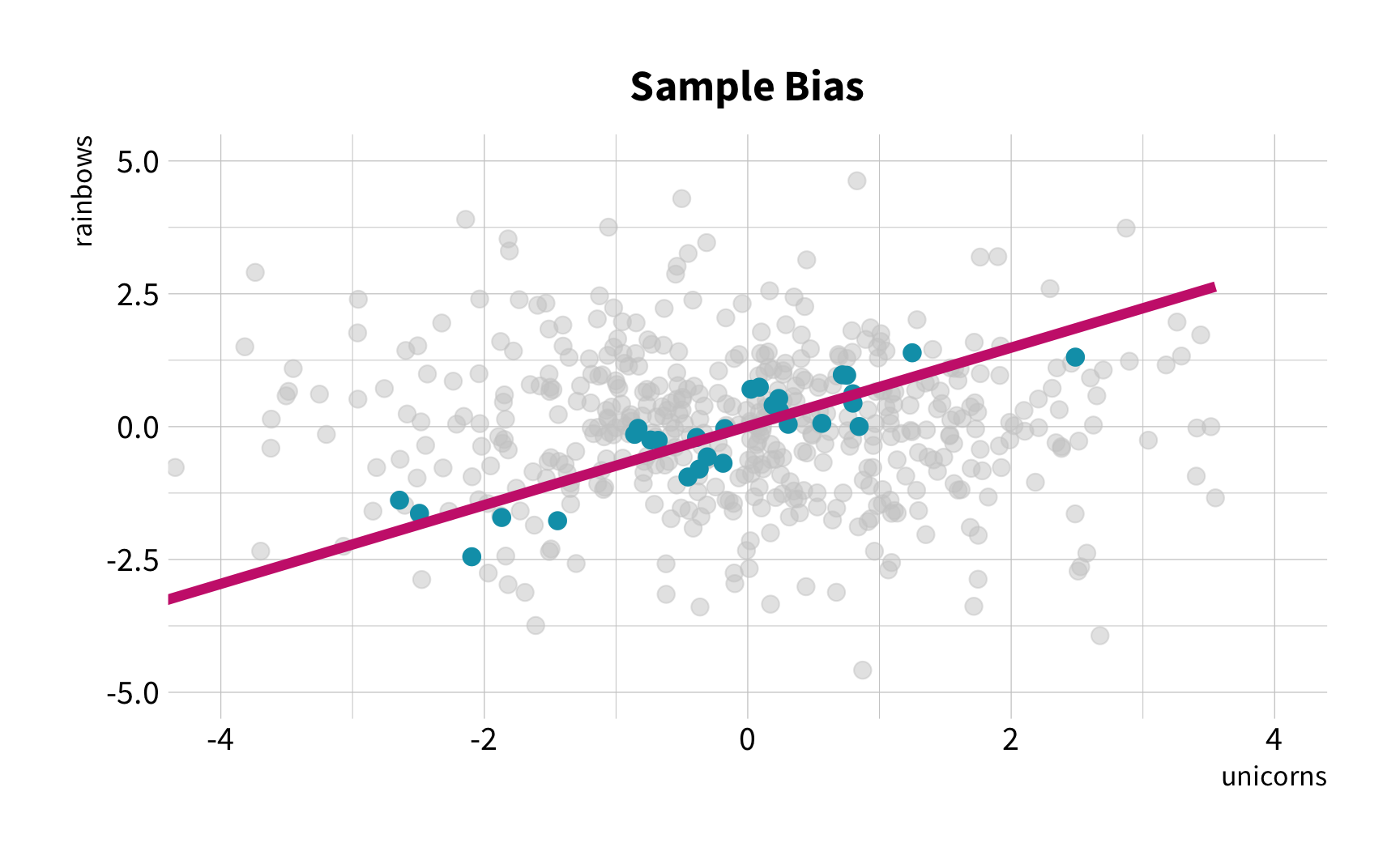
The Solution

Random Sampling

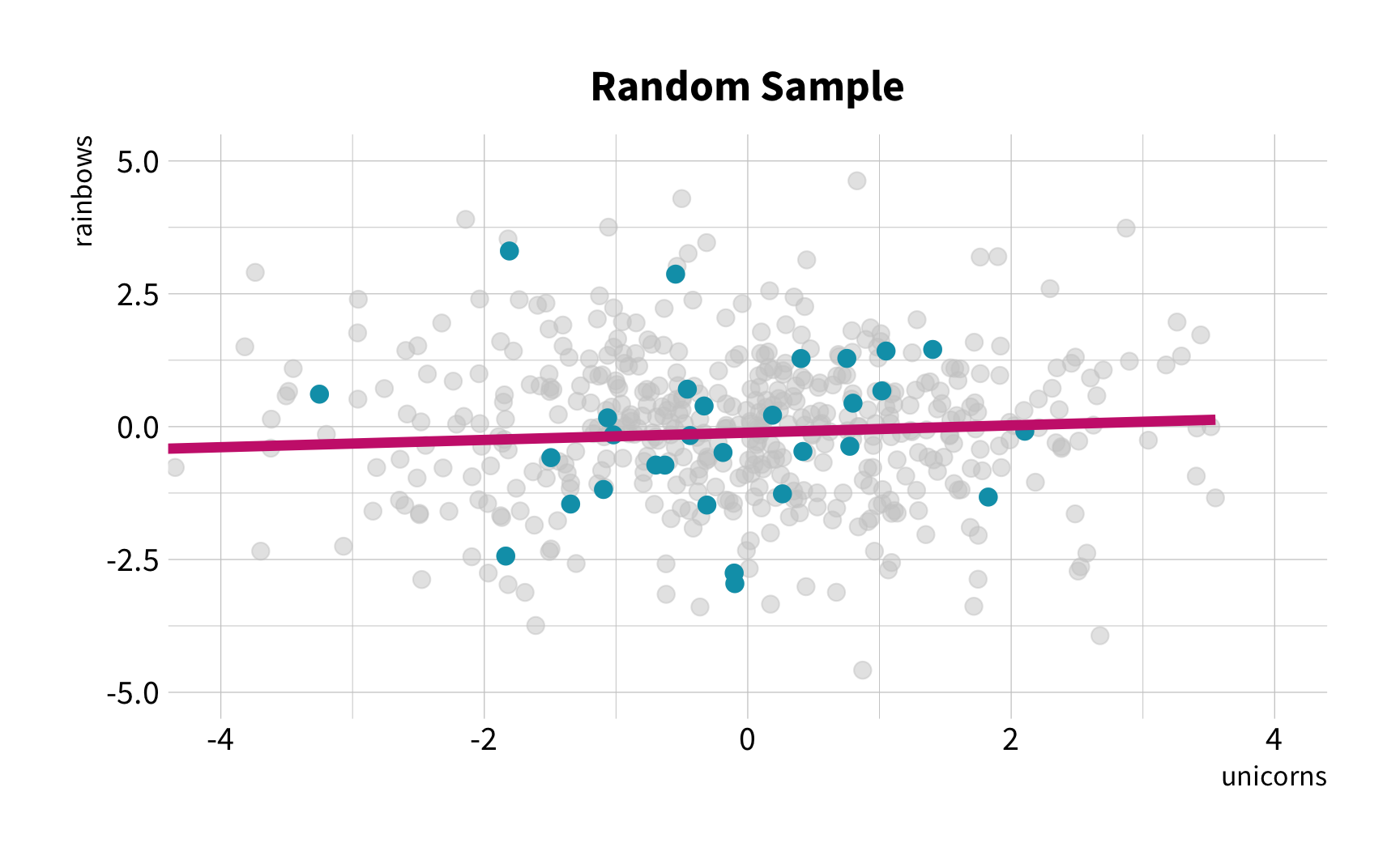
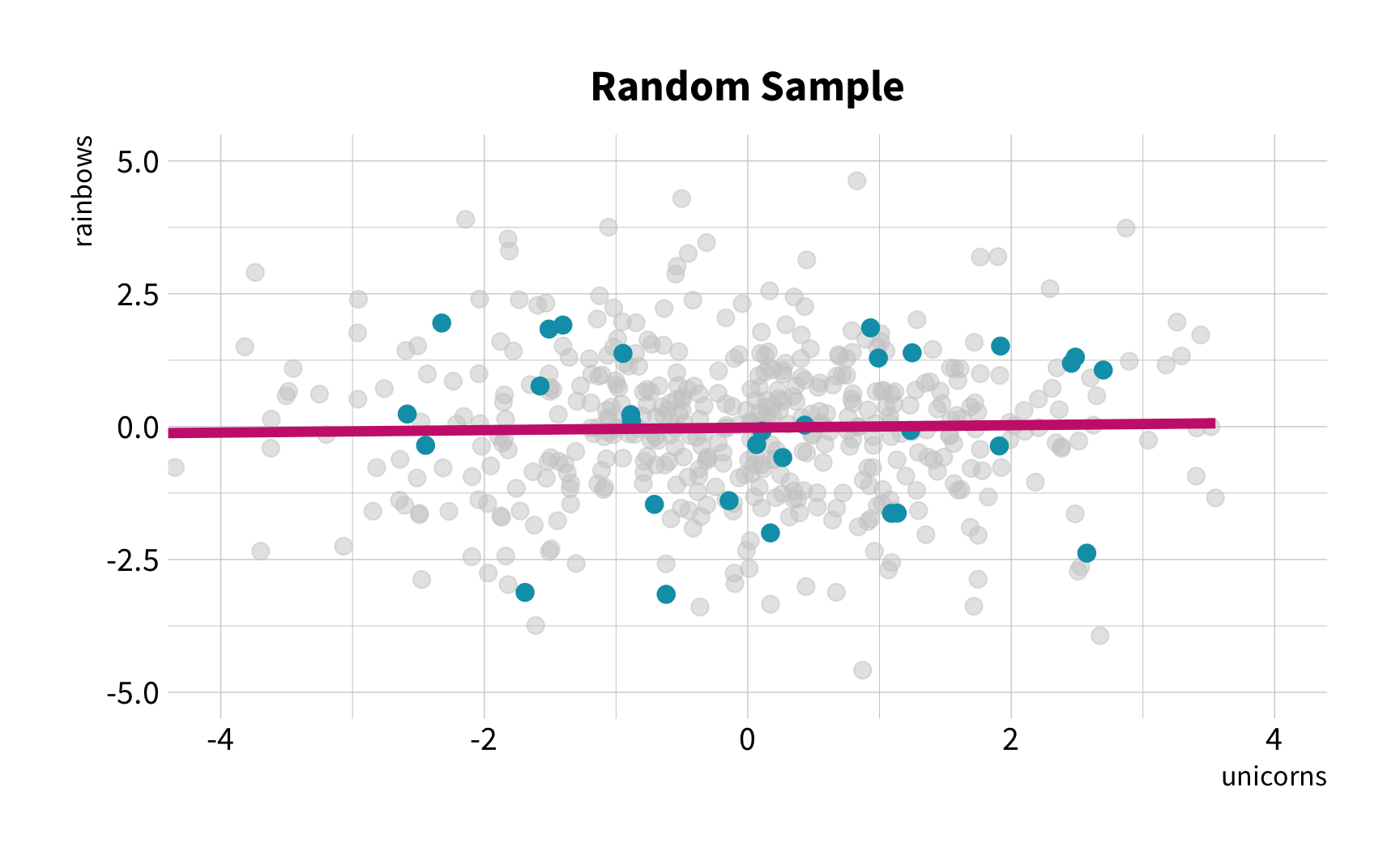
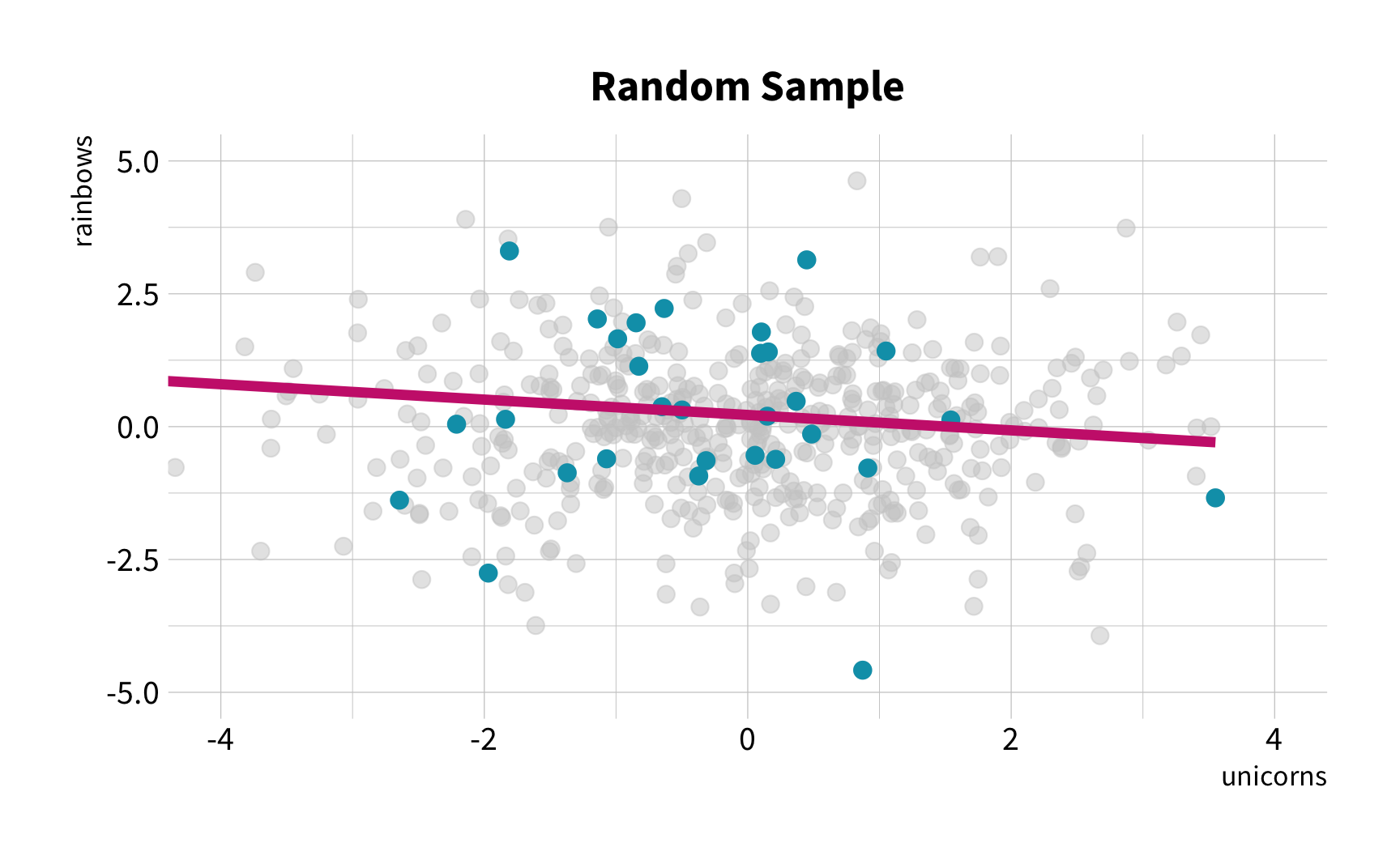
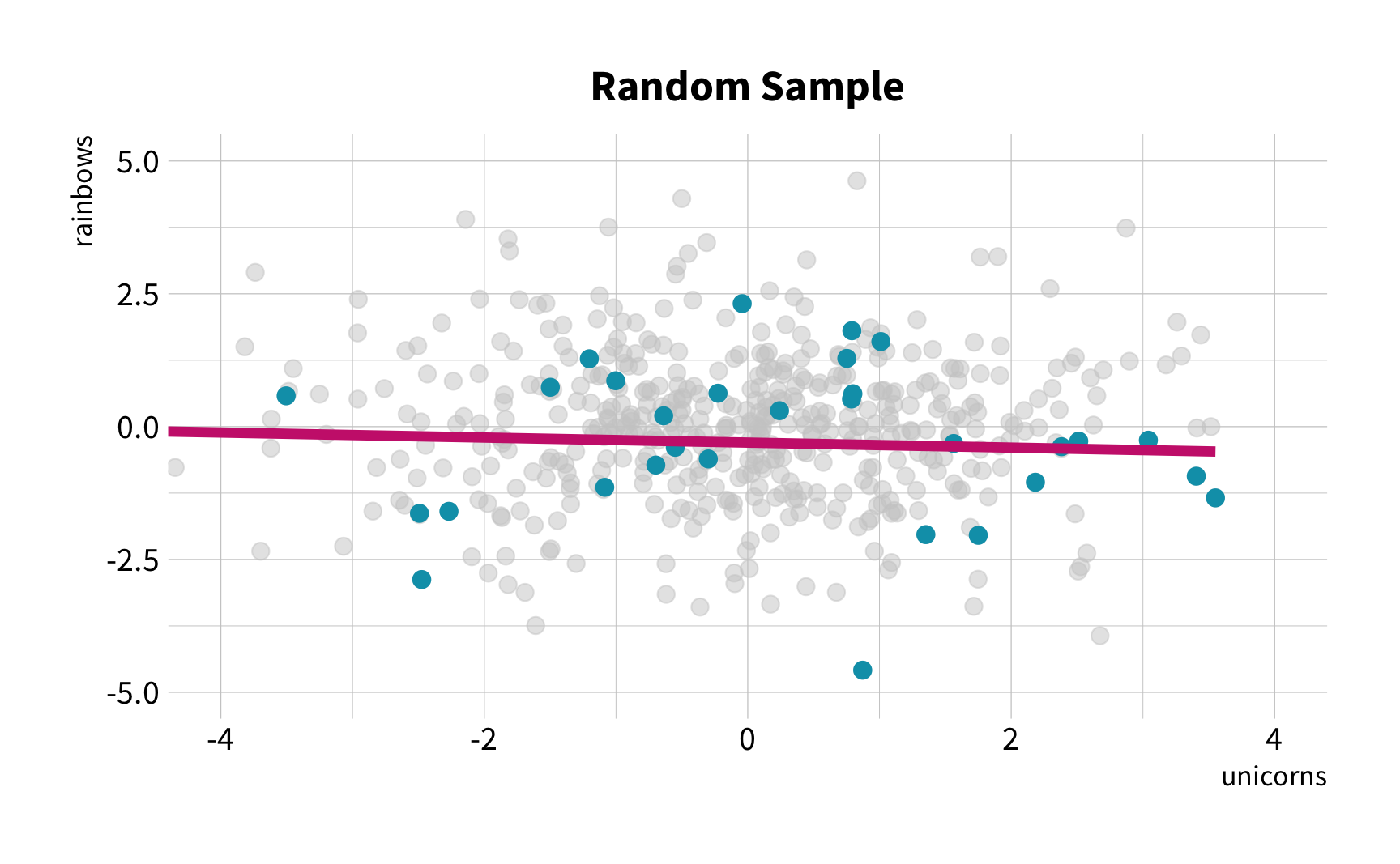
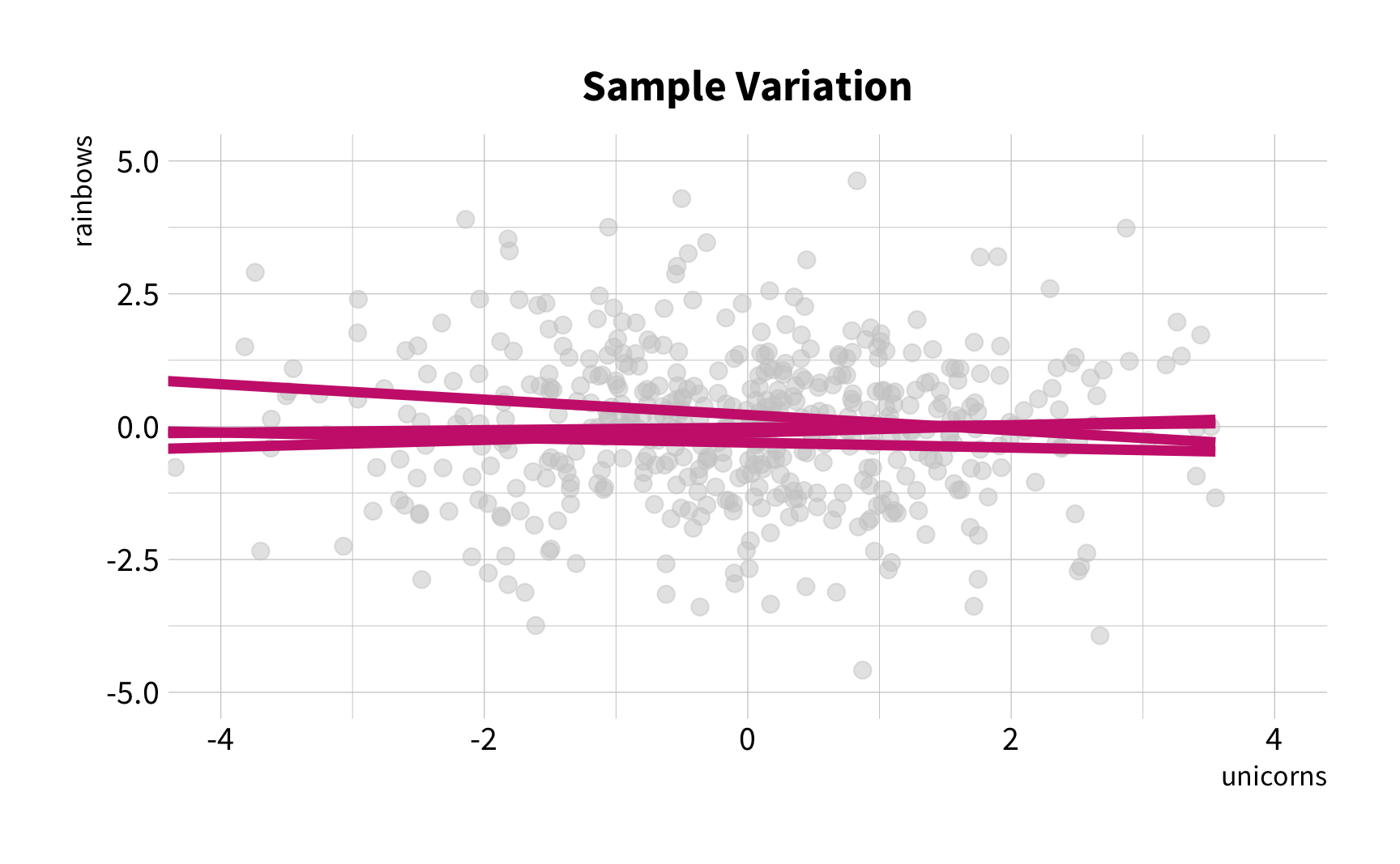
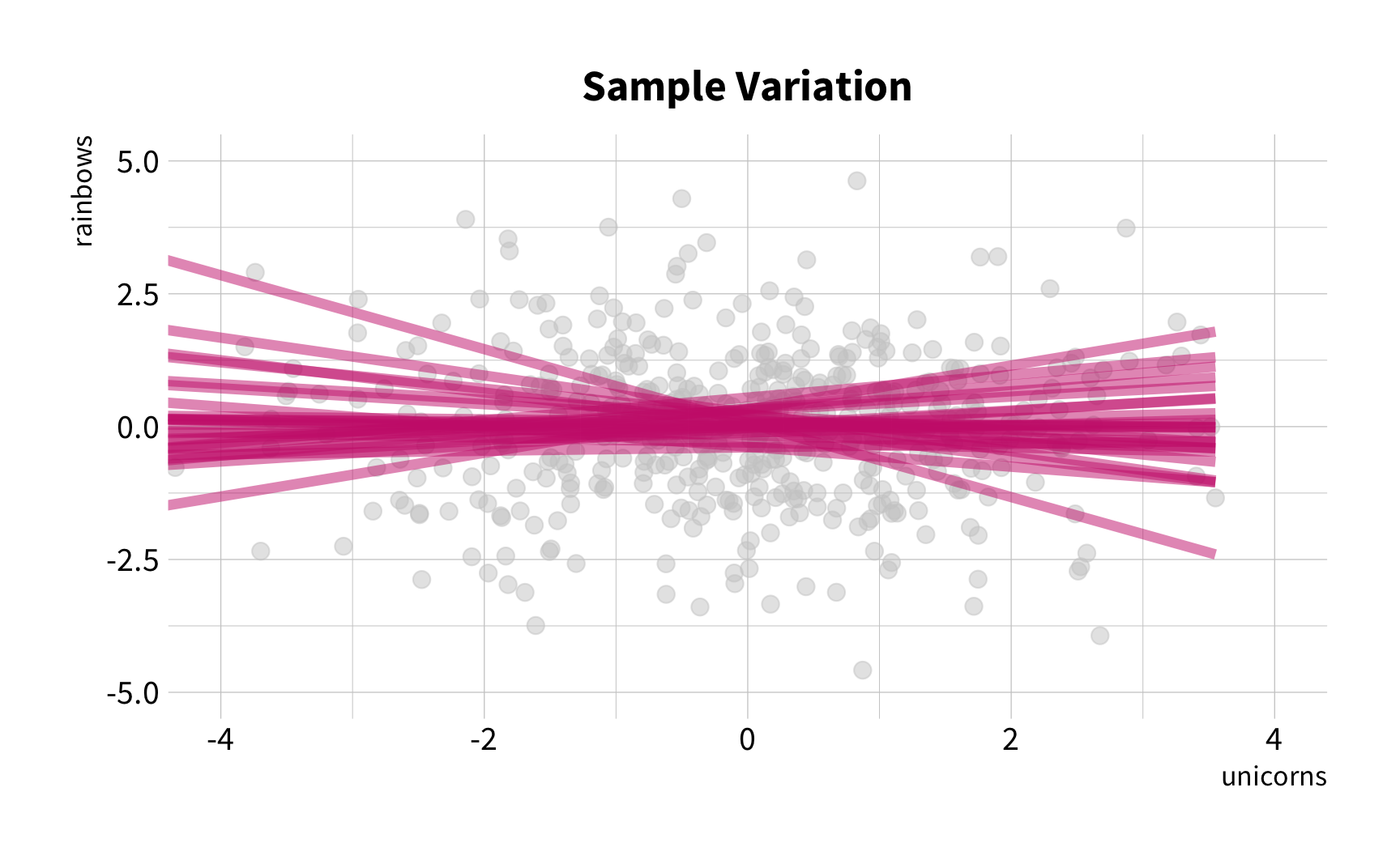
The New Challenge

Sample Variation

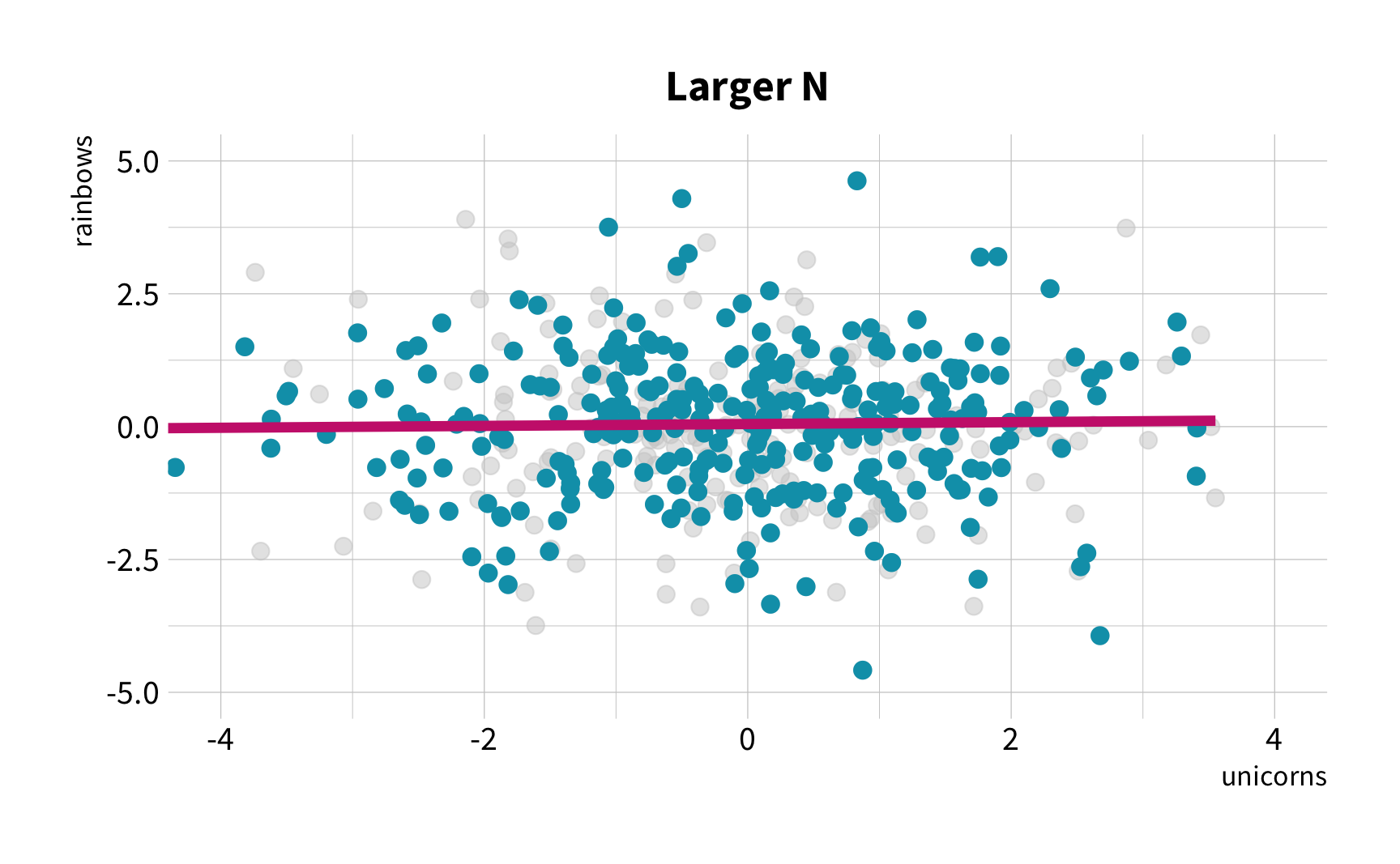
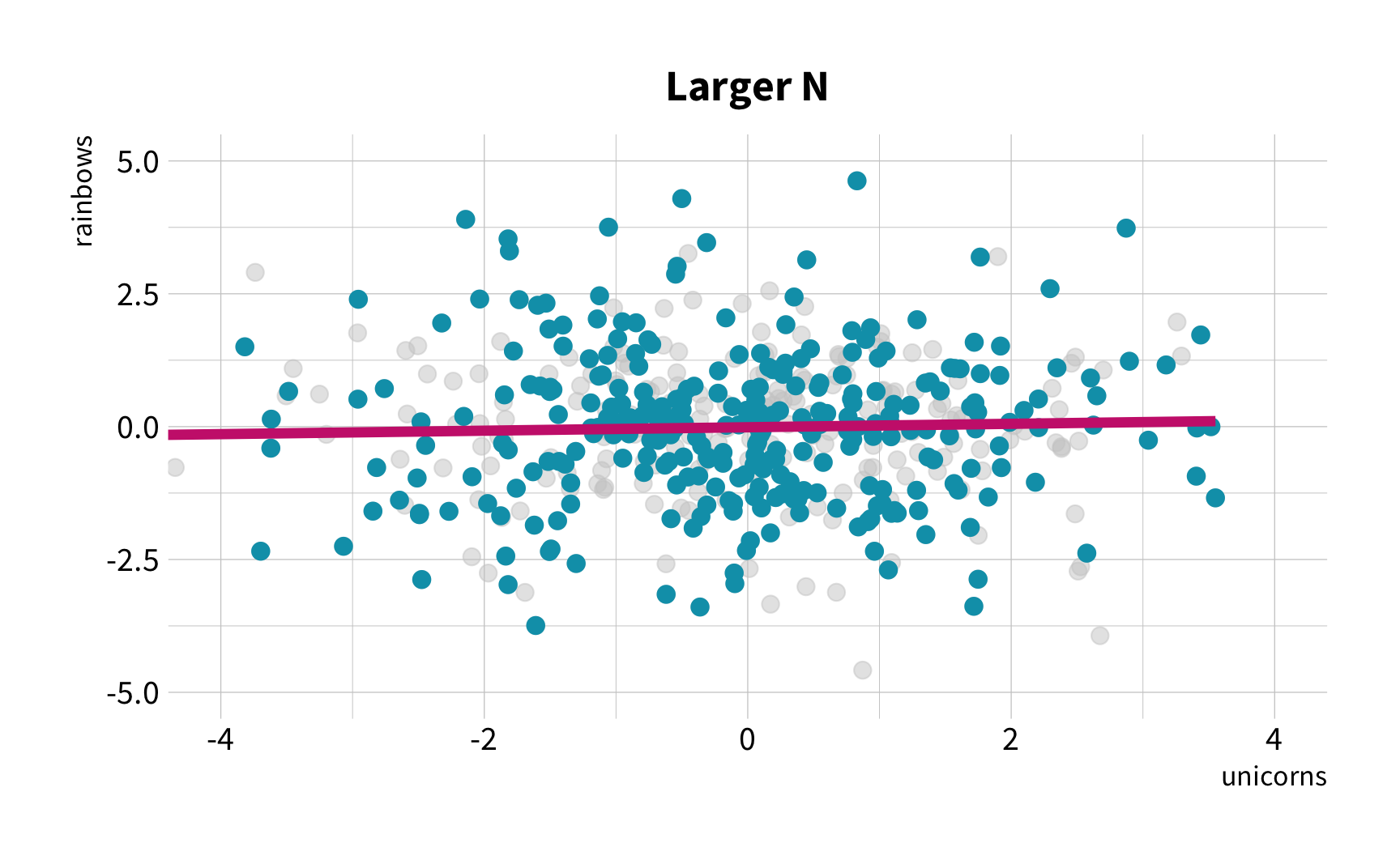
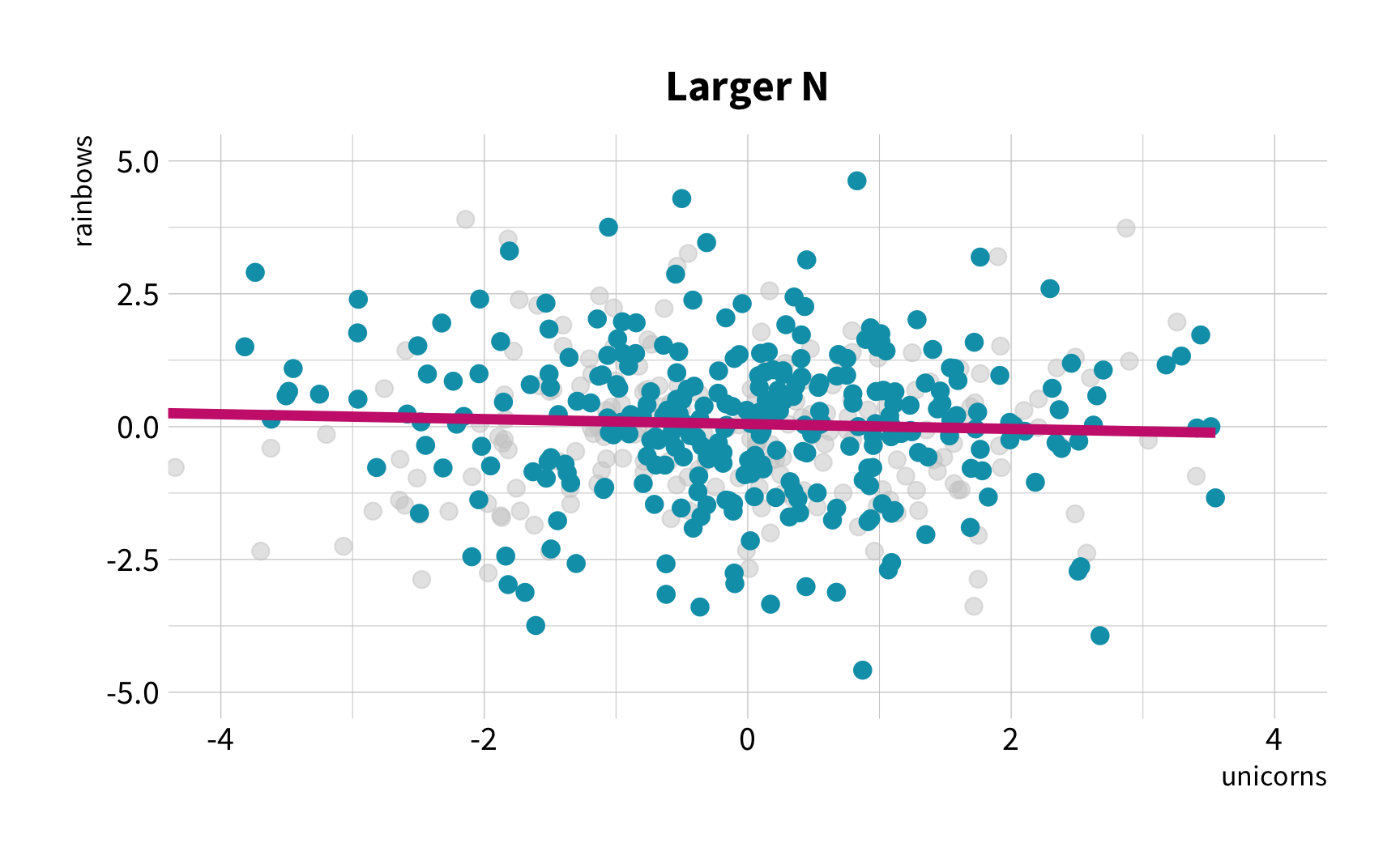
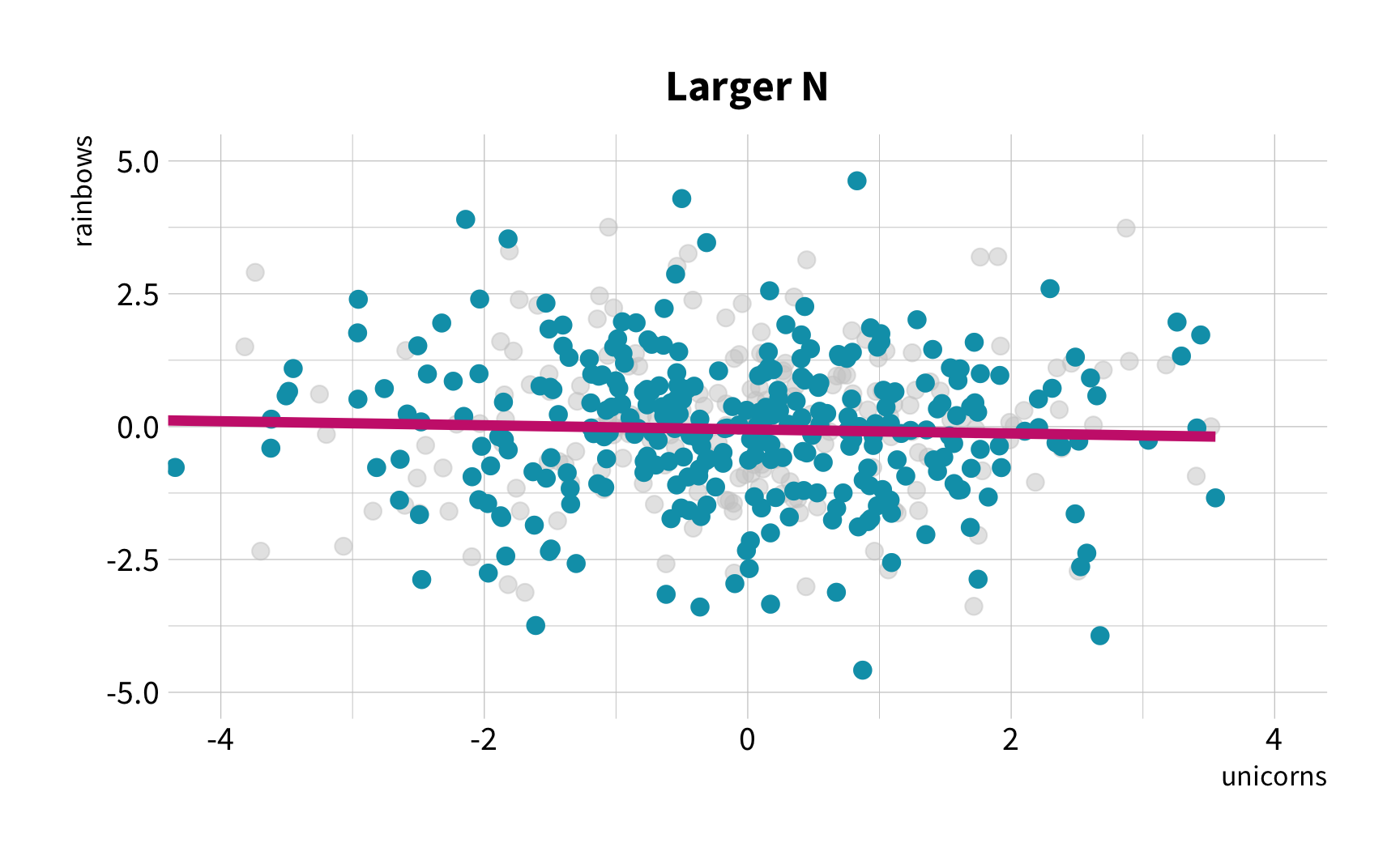
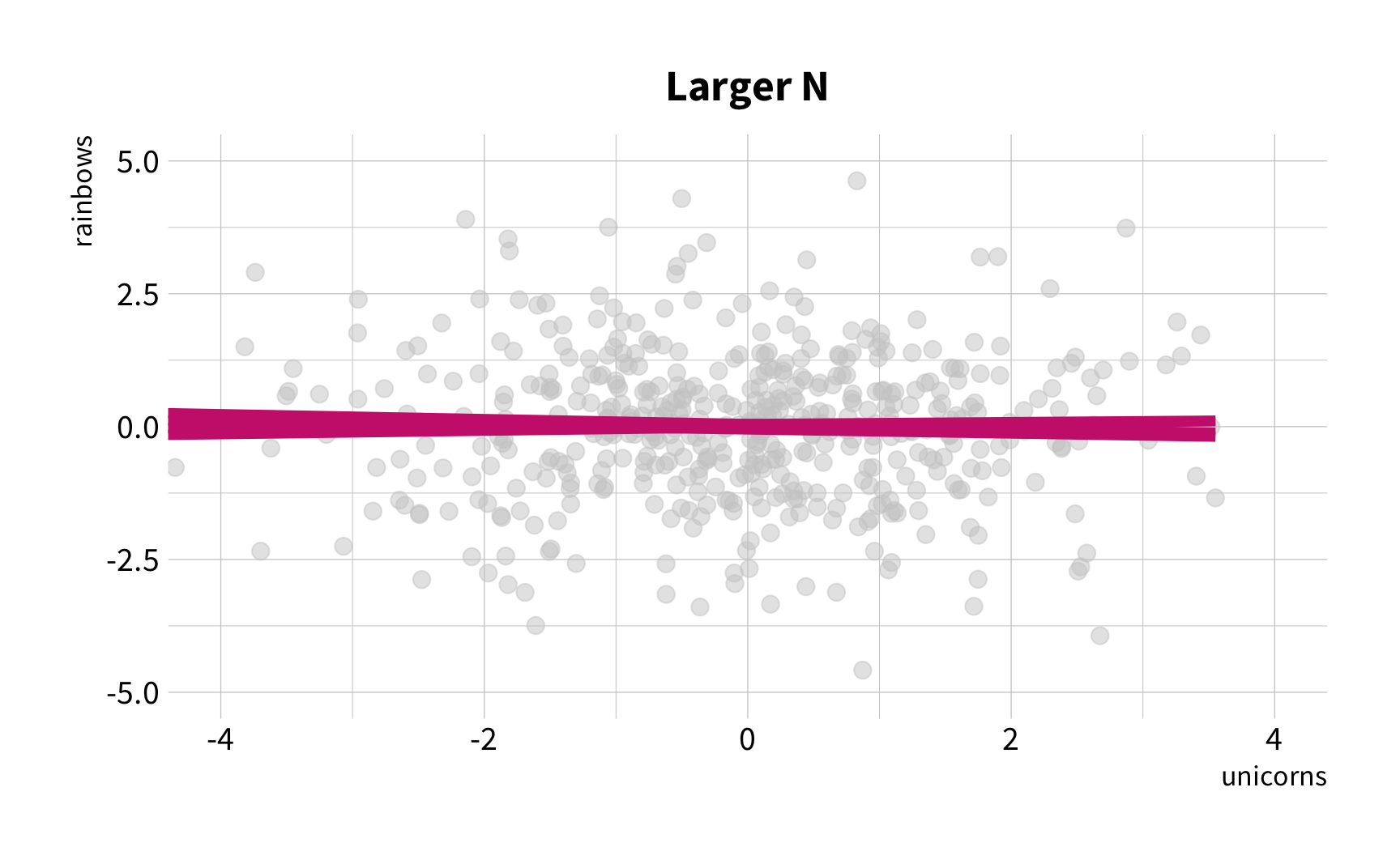
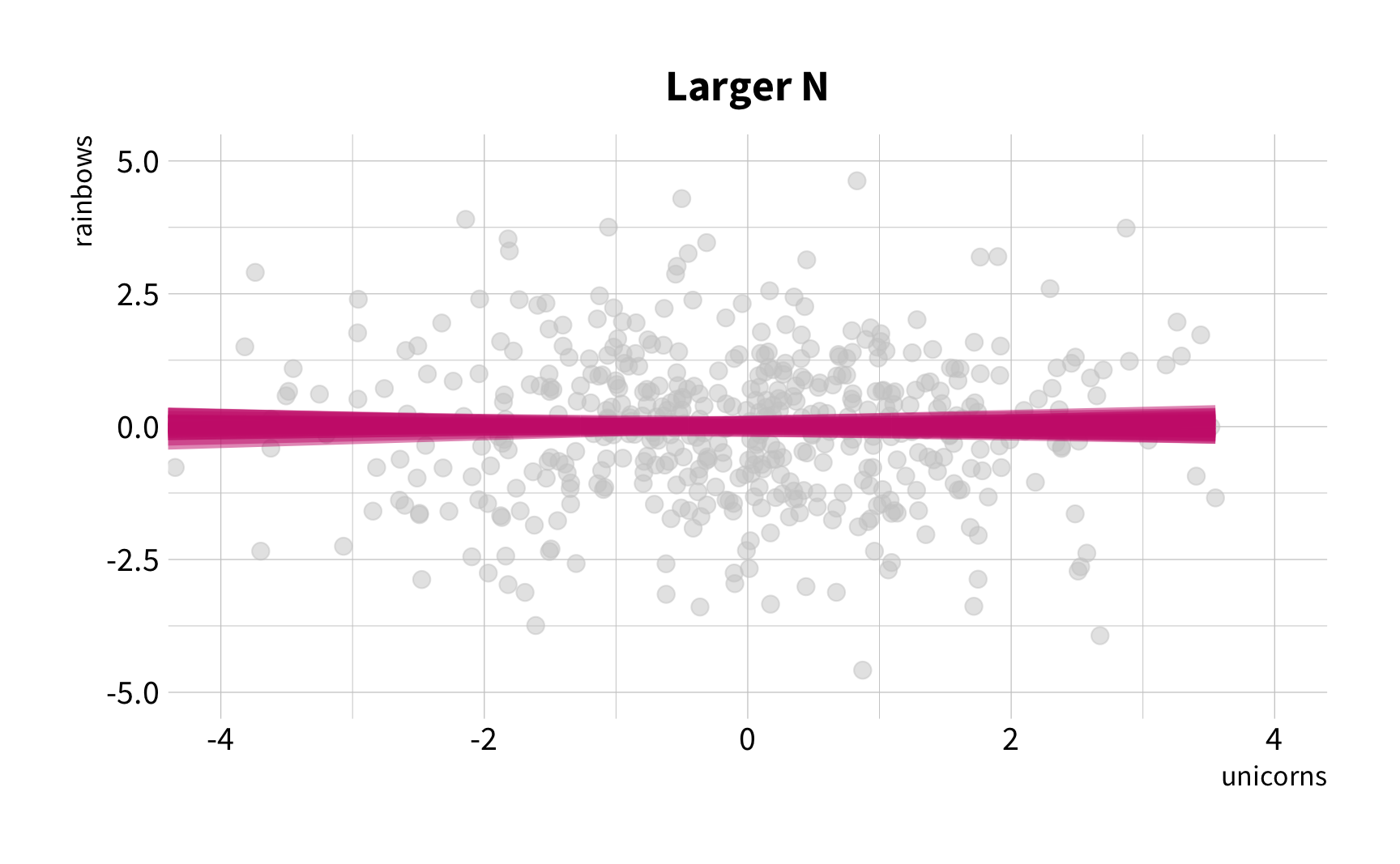
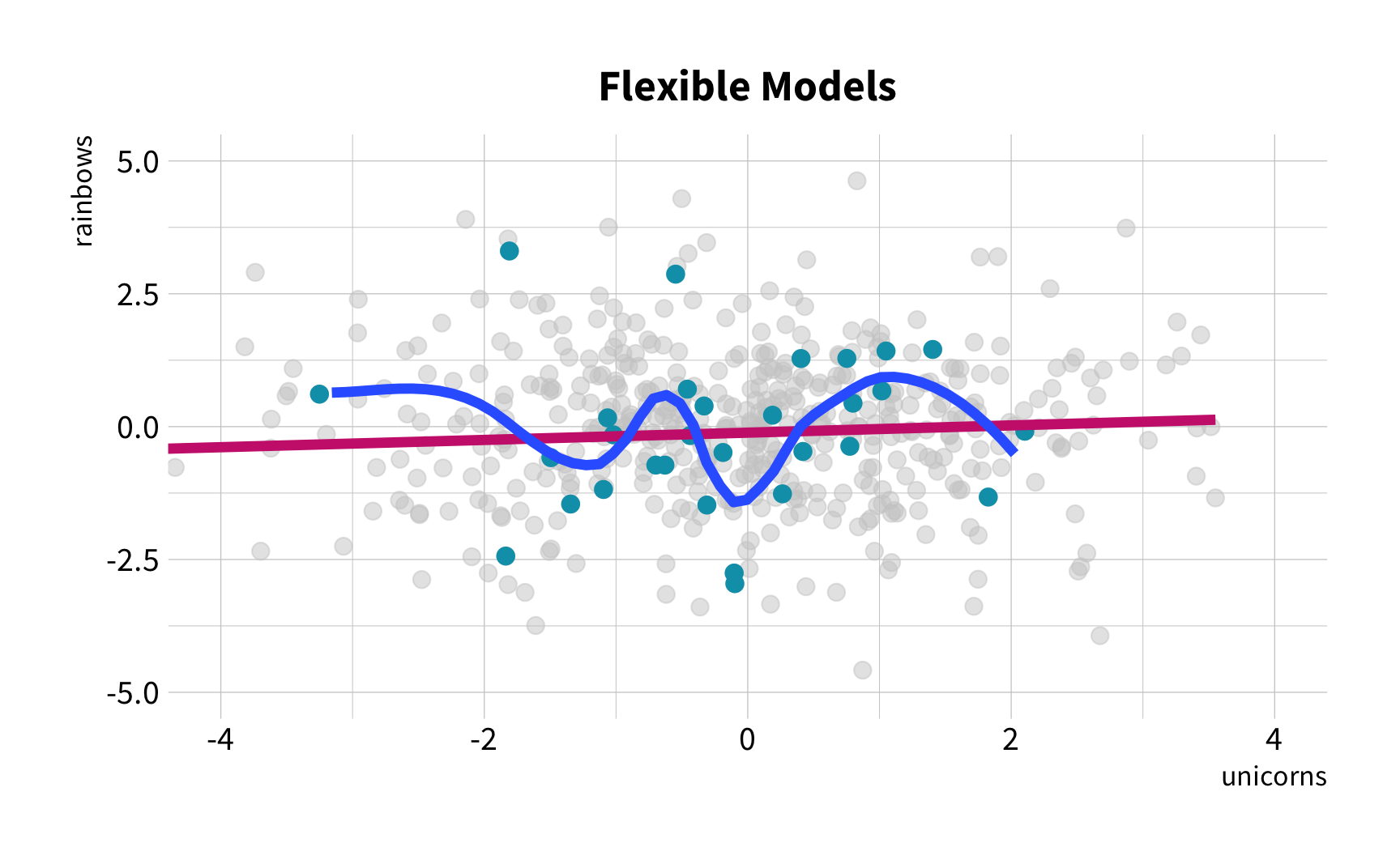
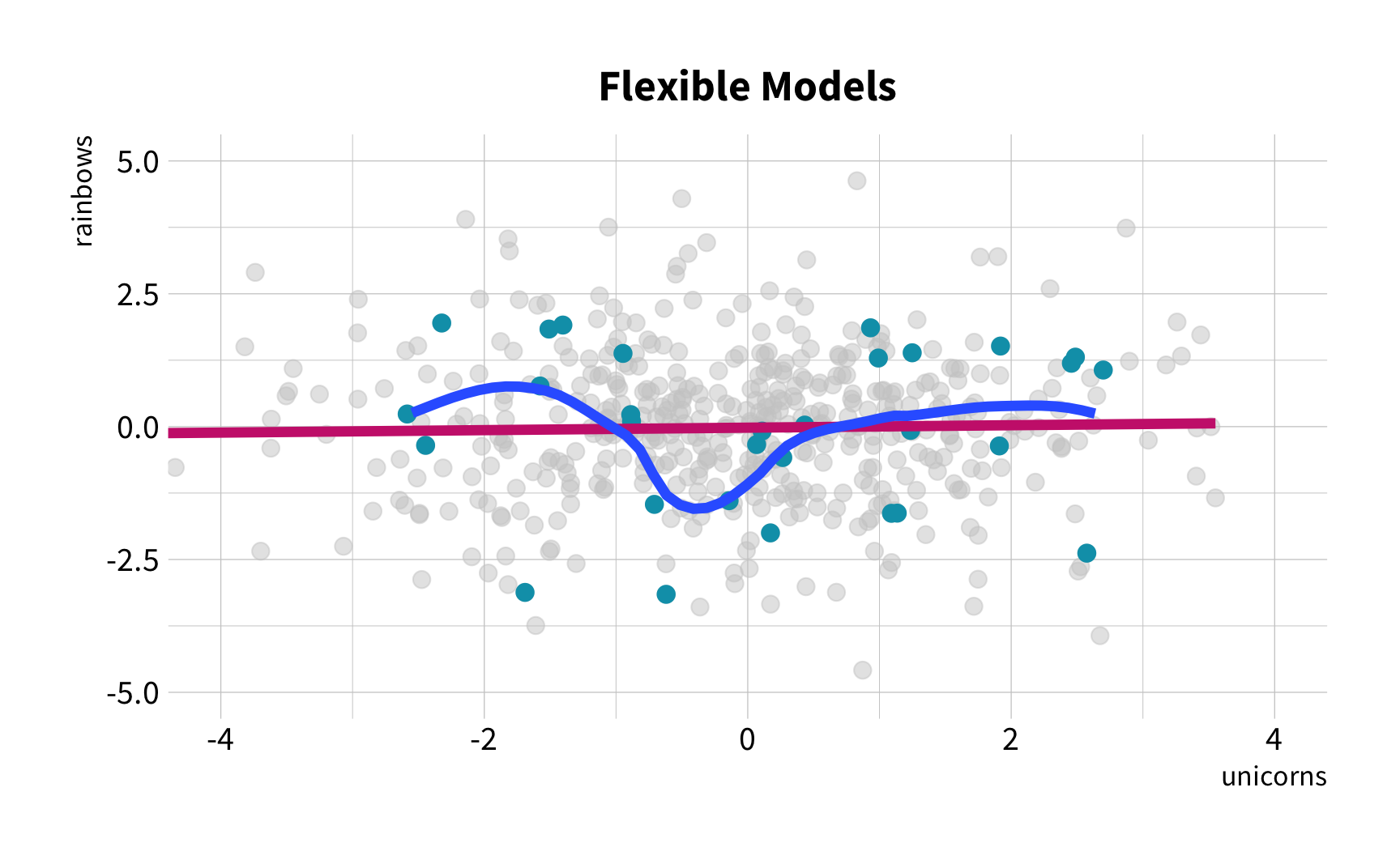
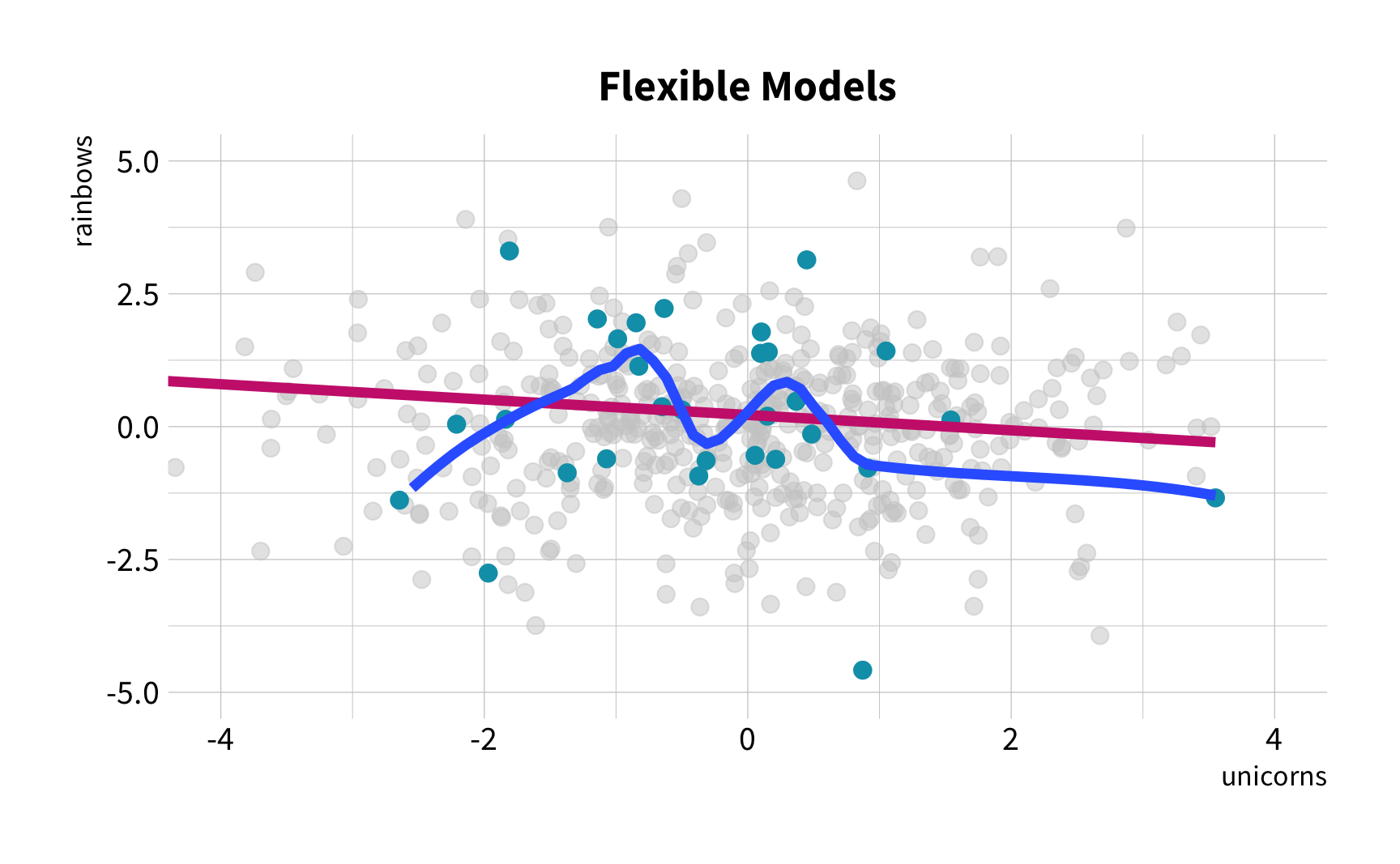
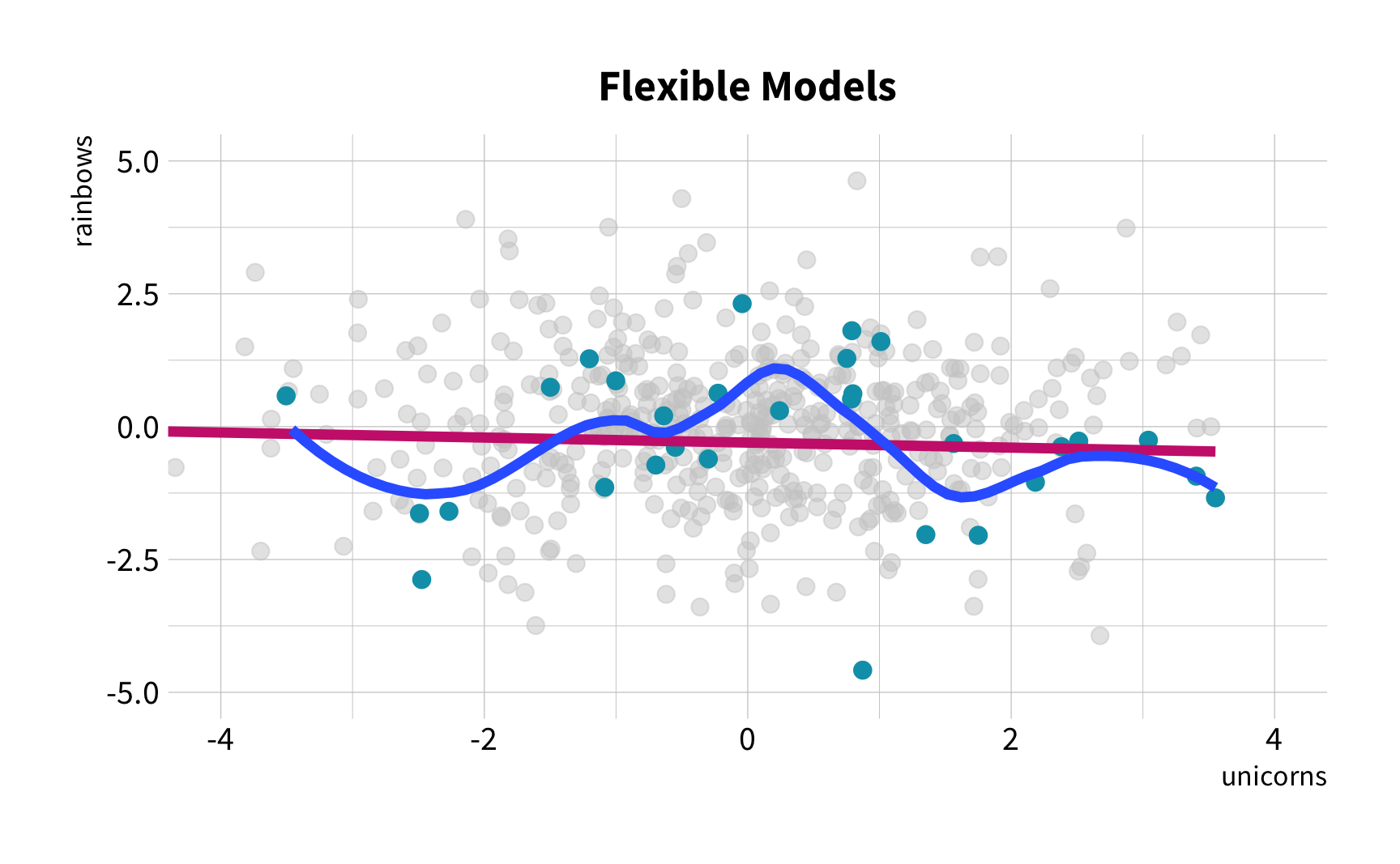
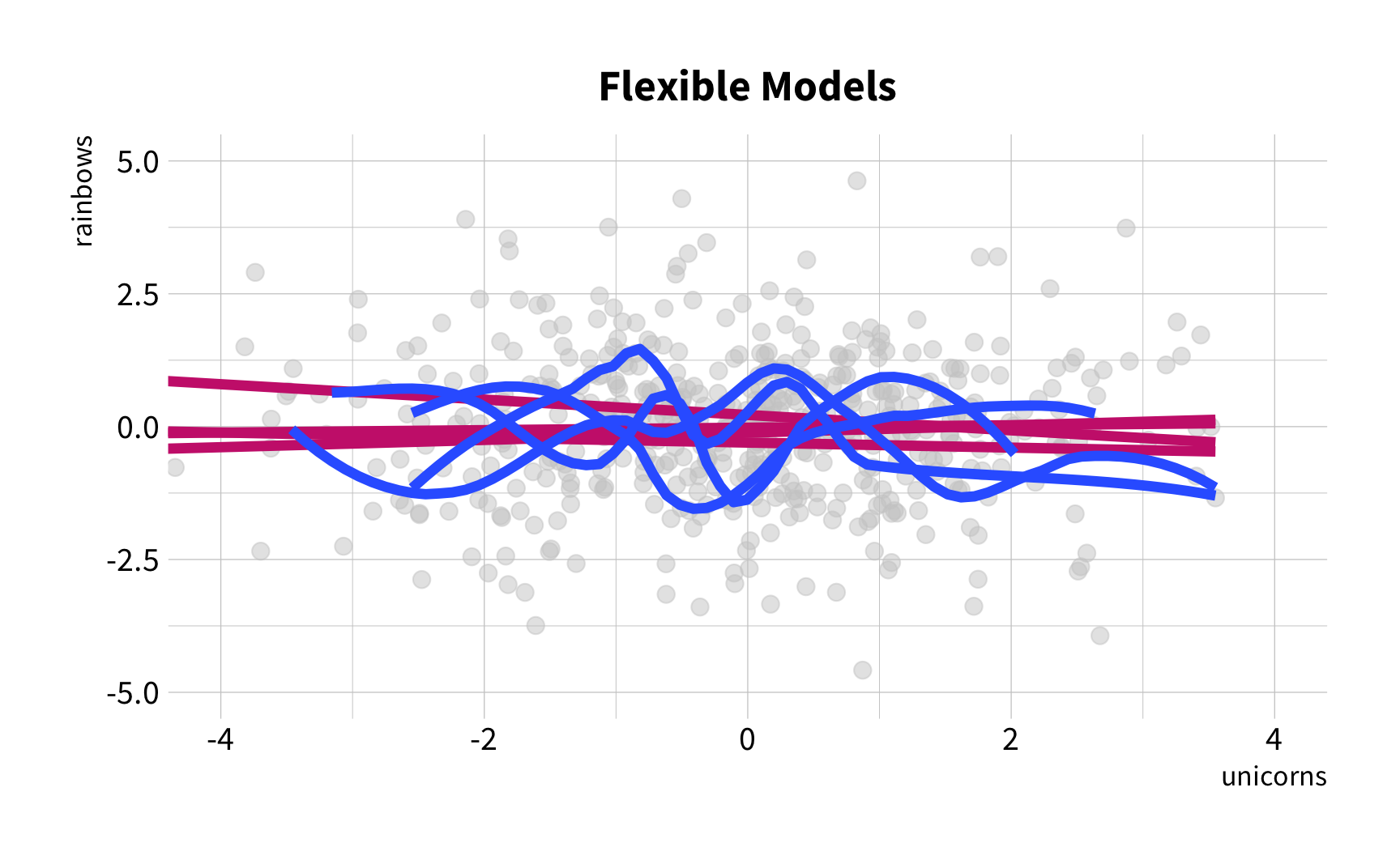
The good news

You don't have to collect more data.

You don't have to sacrifice fit for flexibility.

Palmer Penguins

Artwork by @allison_horst

[Ah]-dell-ee

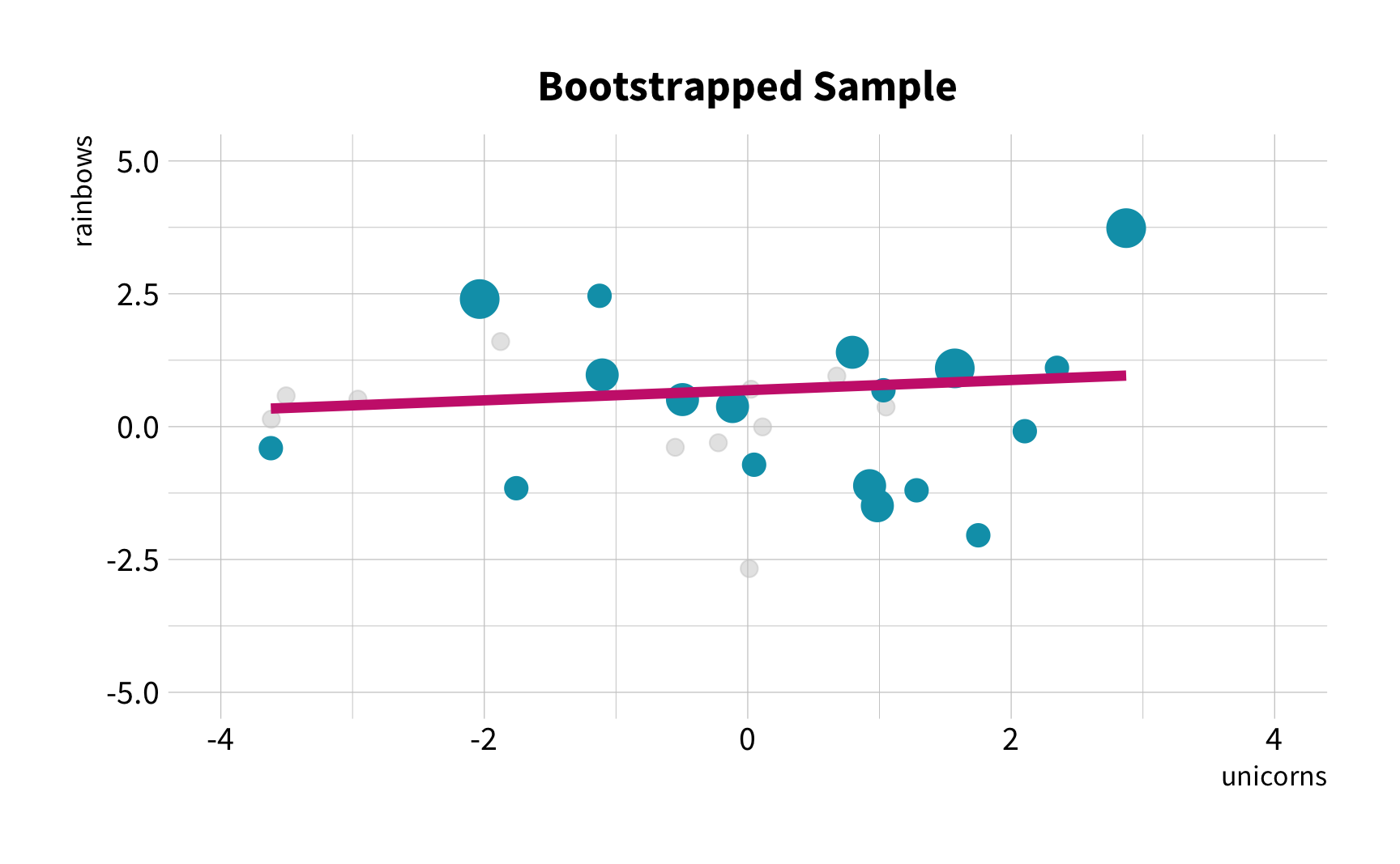
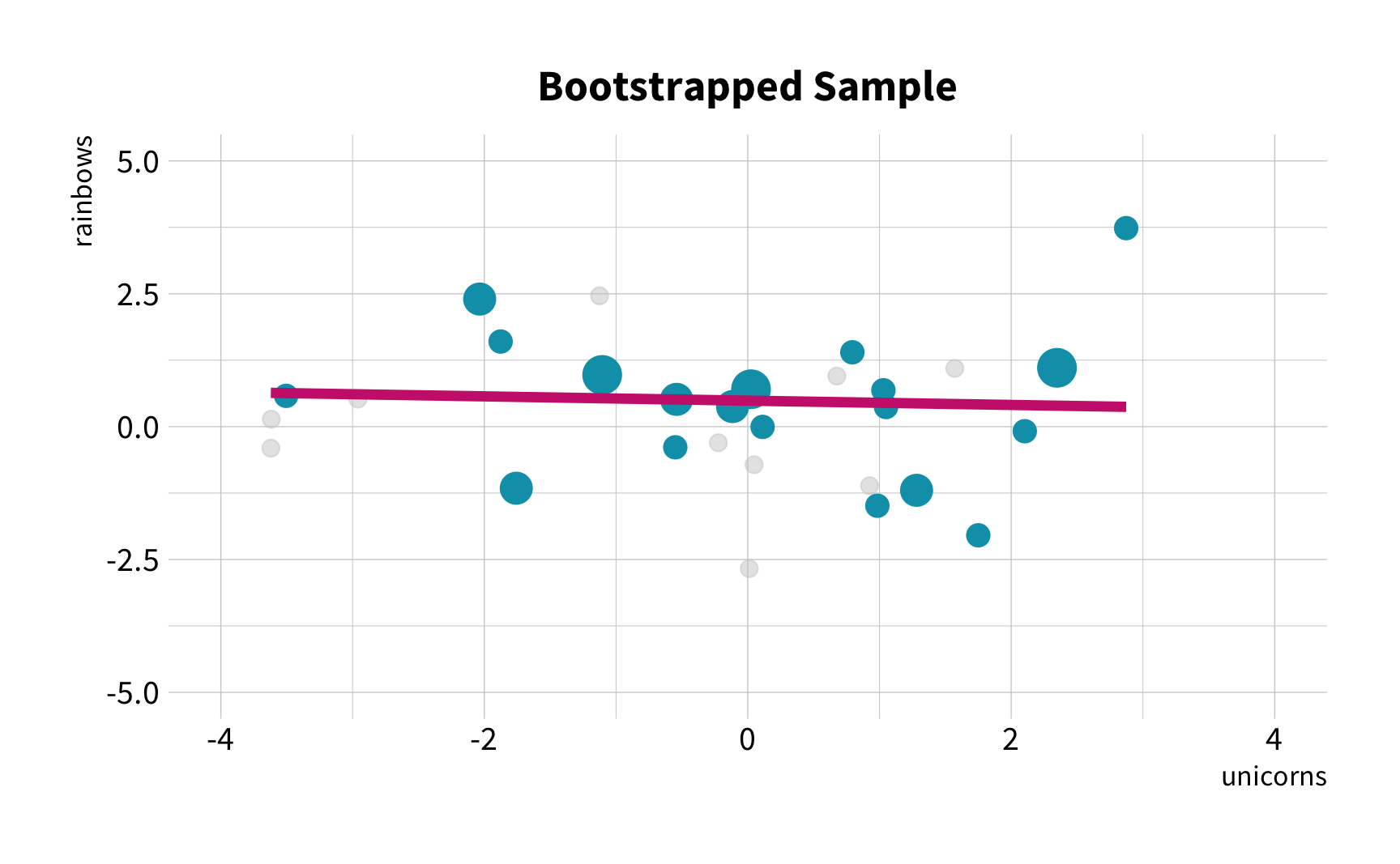
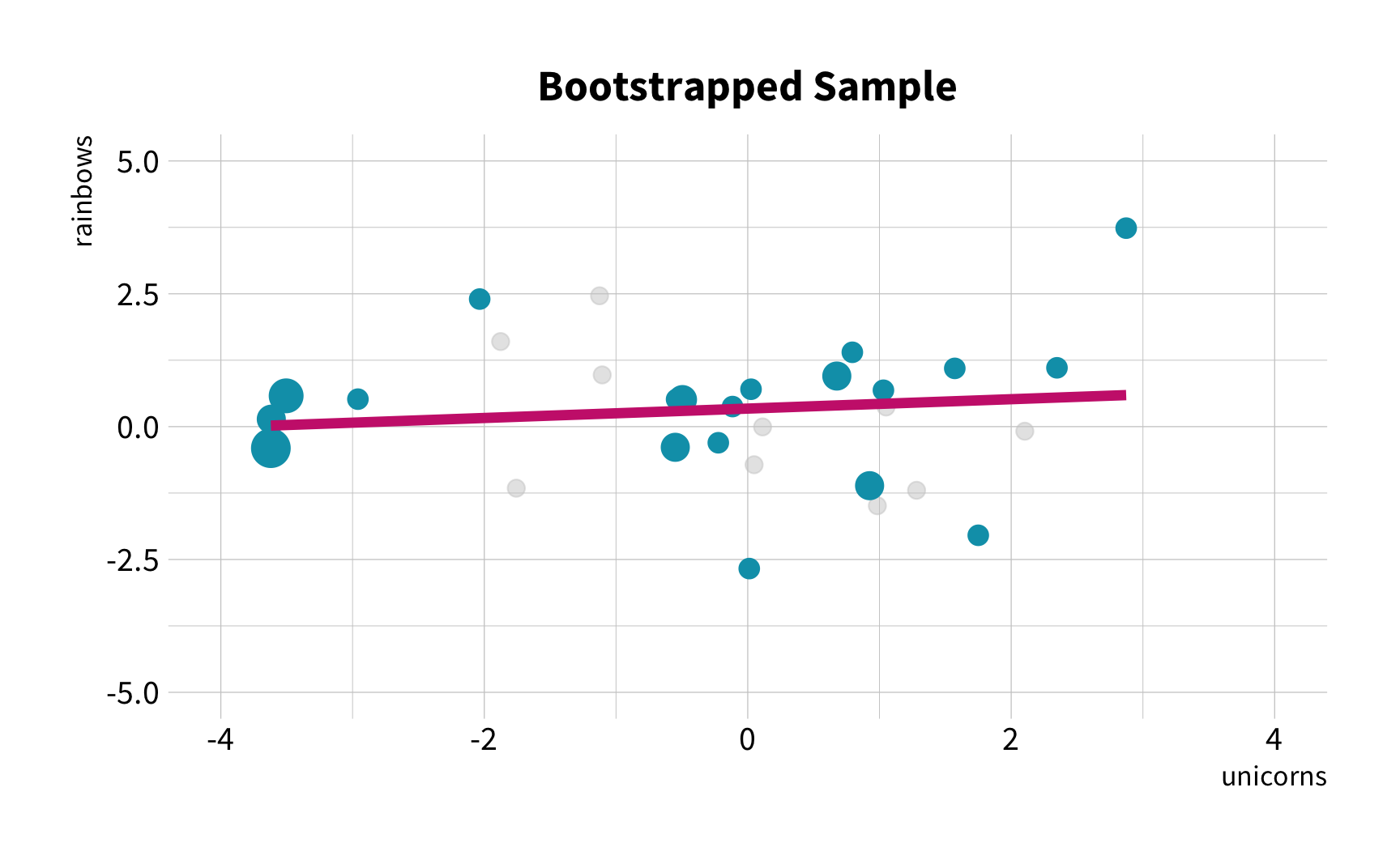
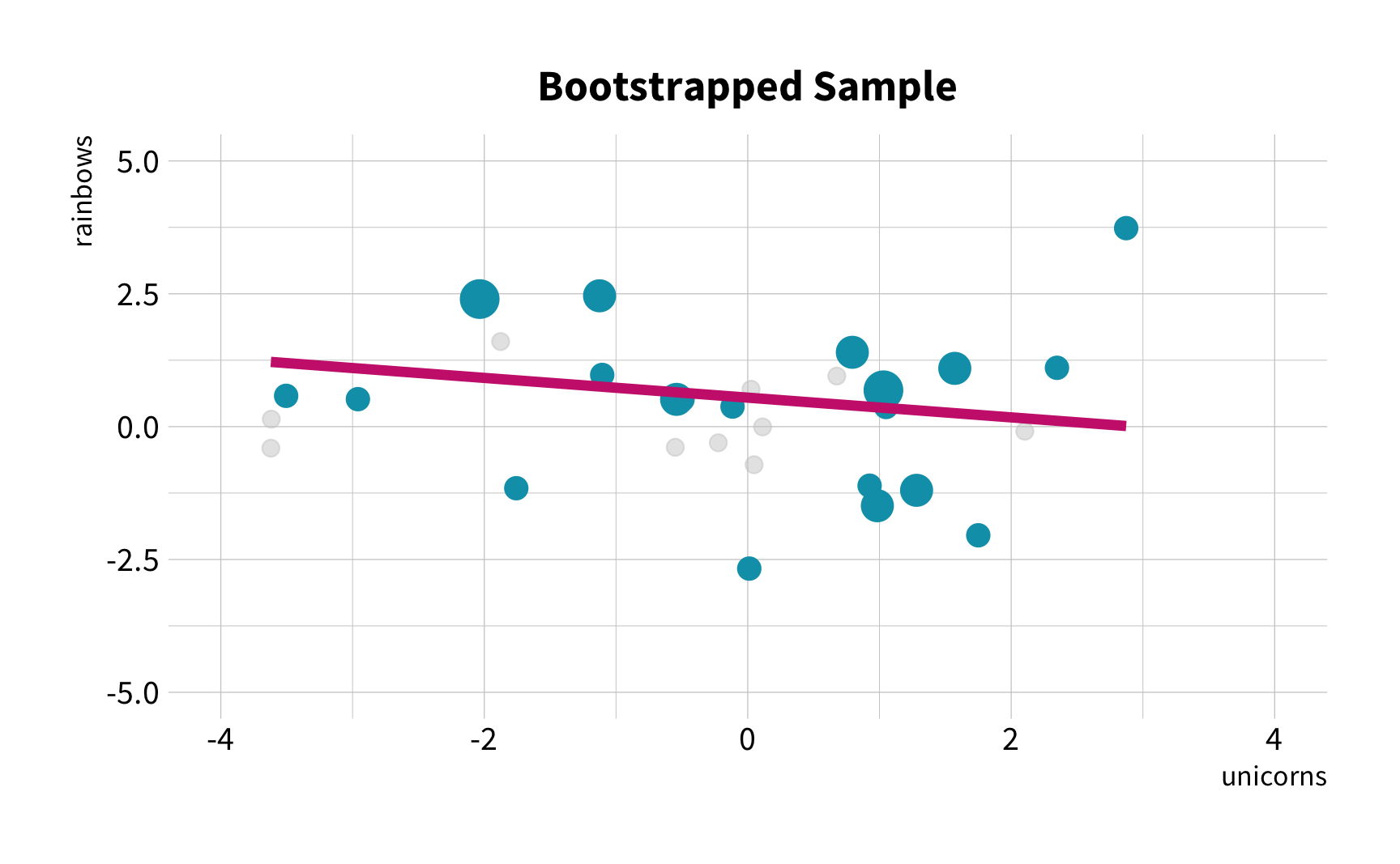
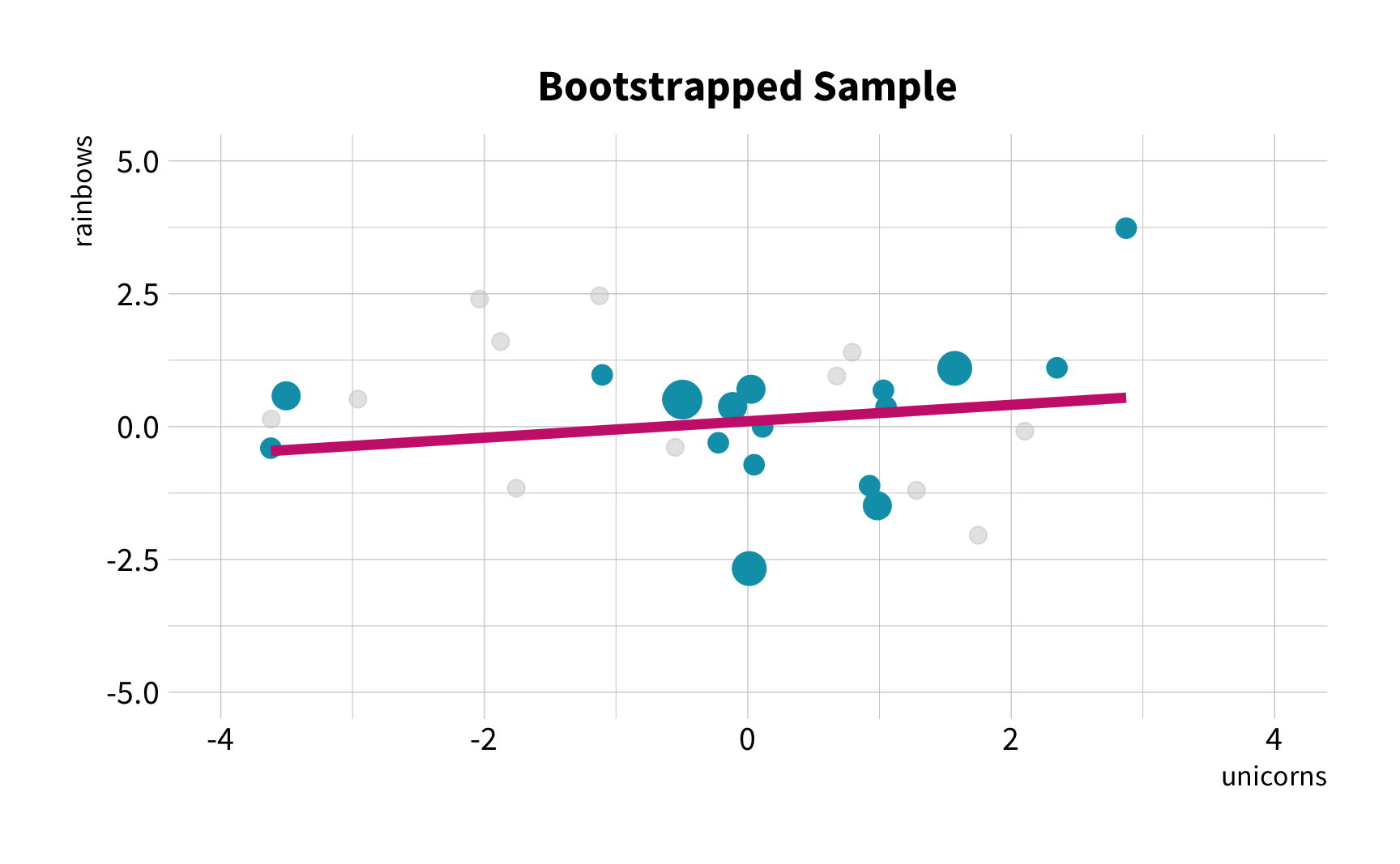
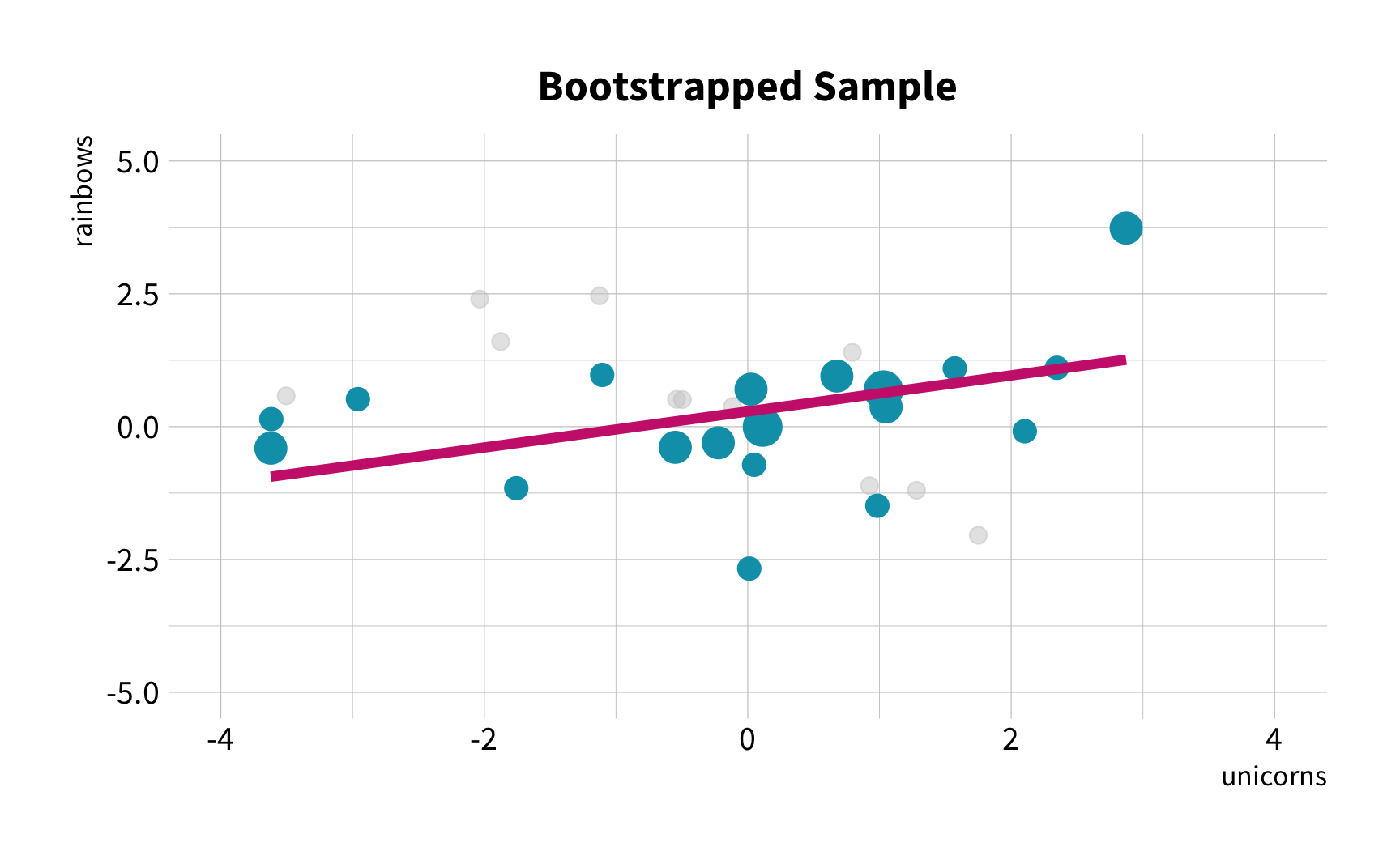
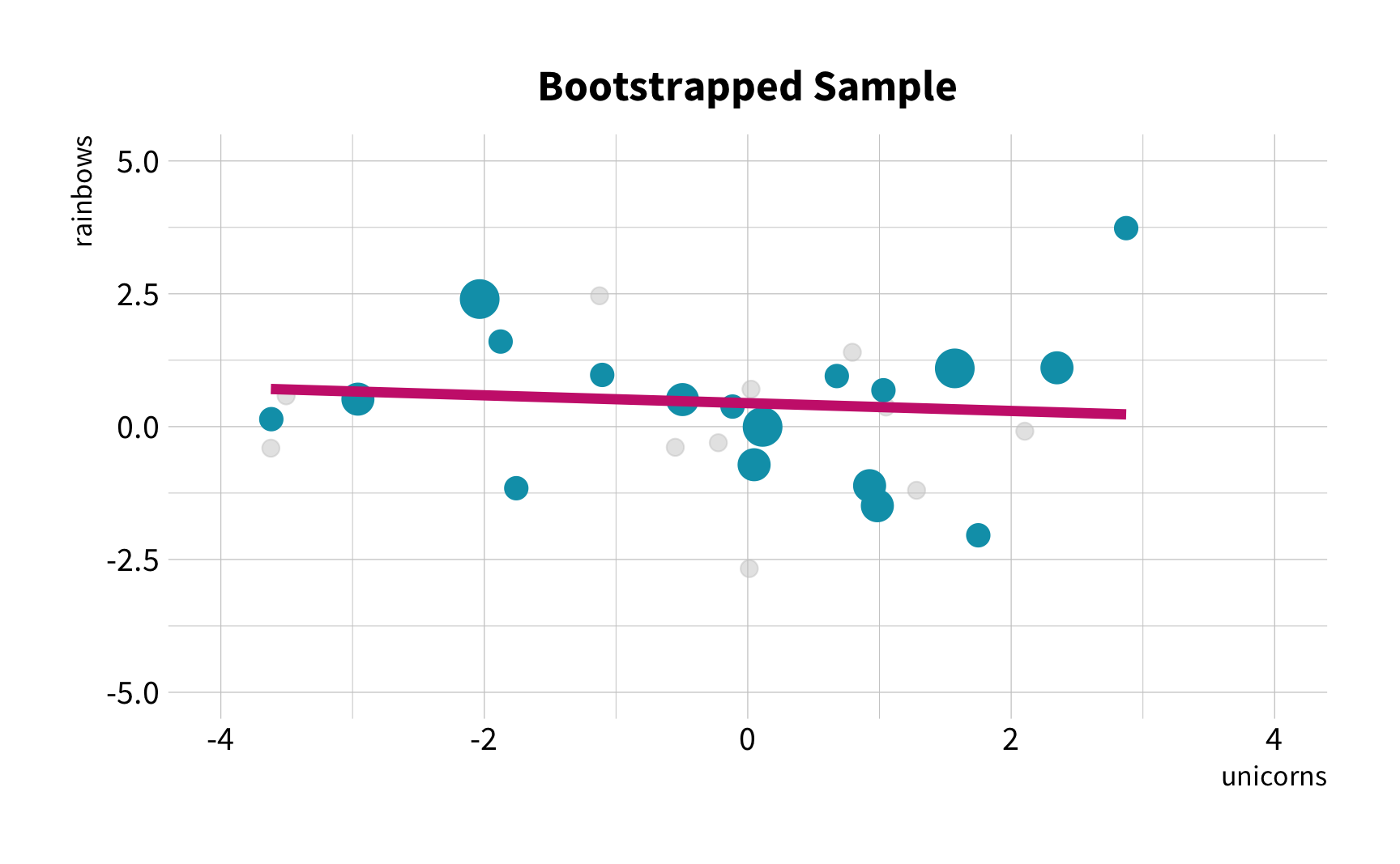
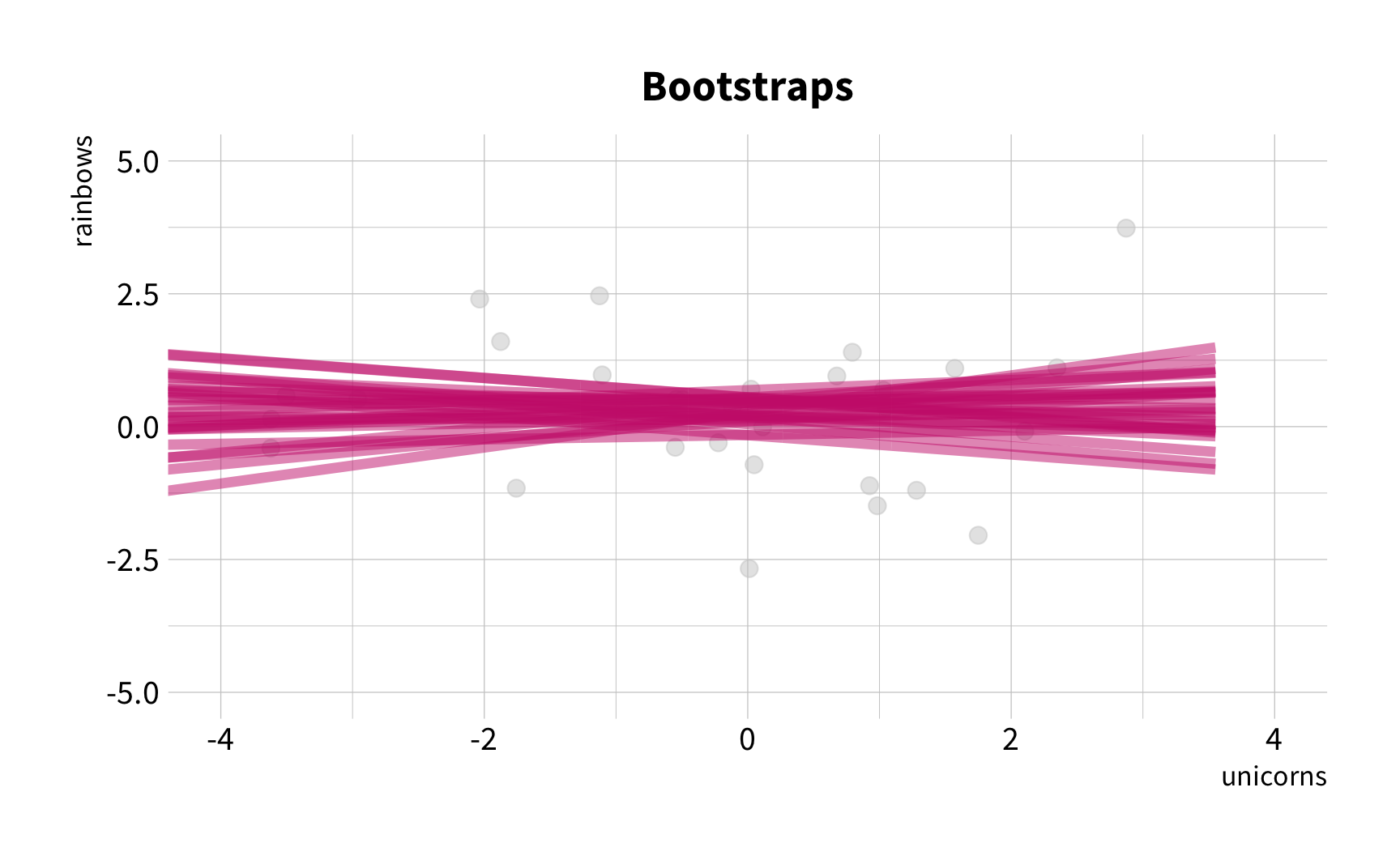
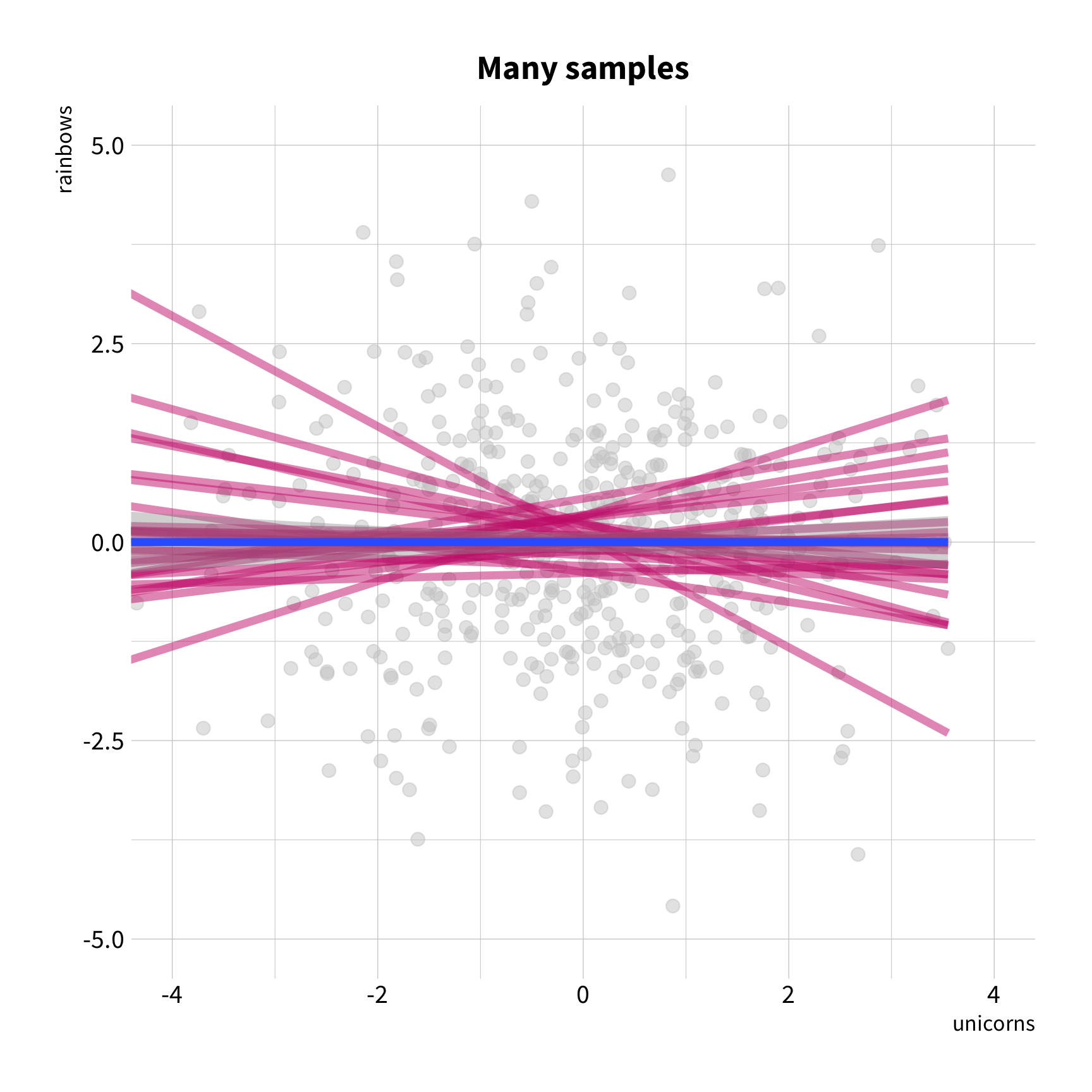
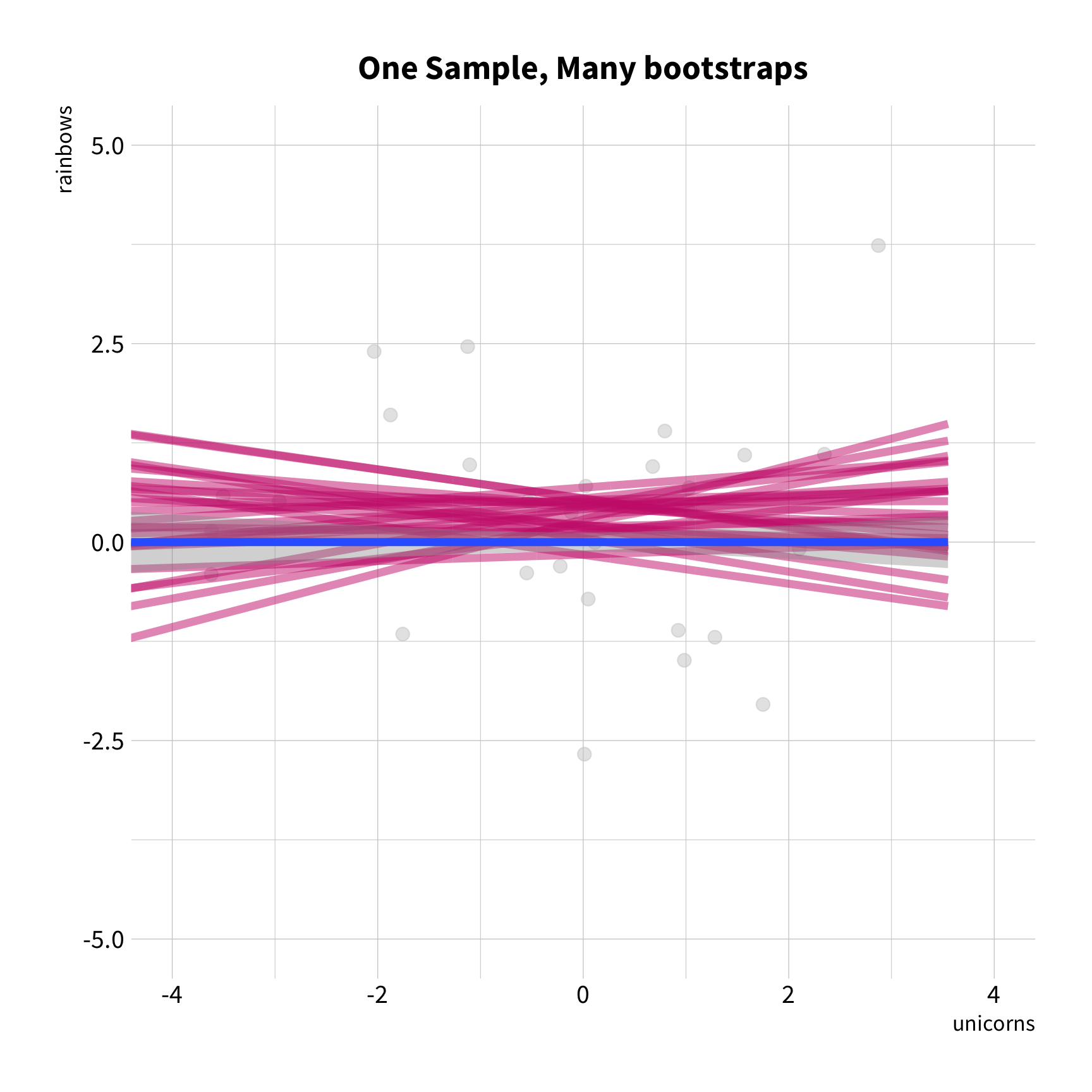
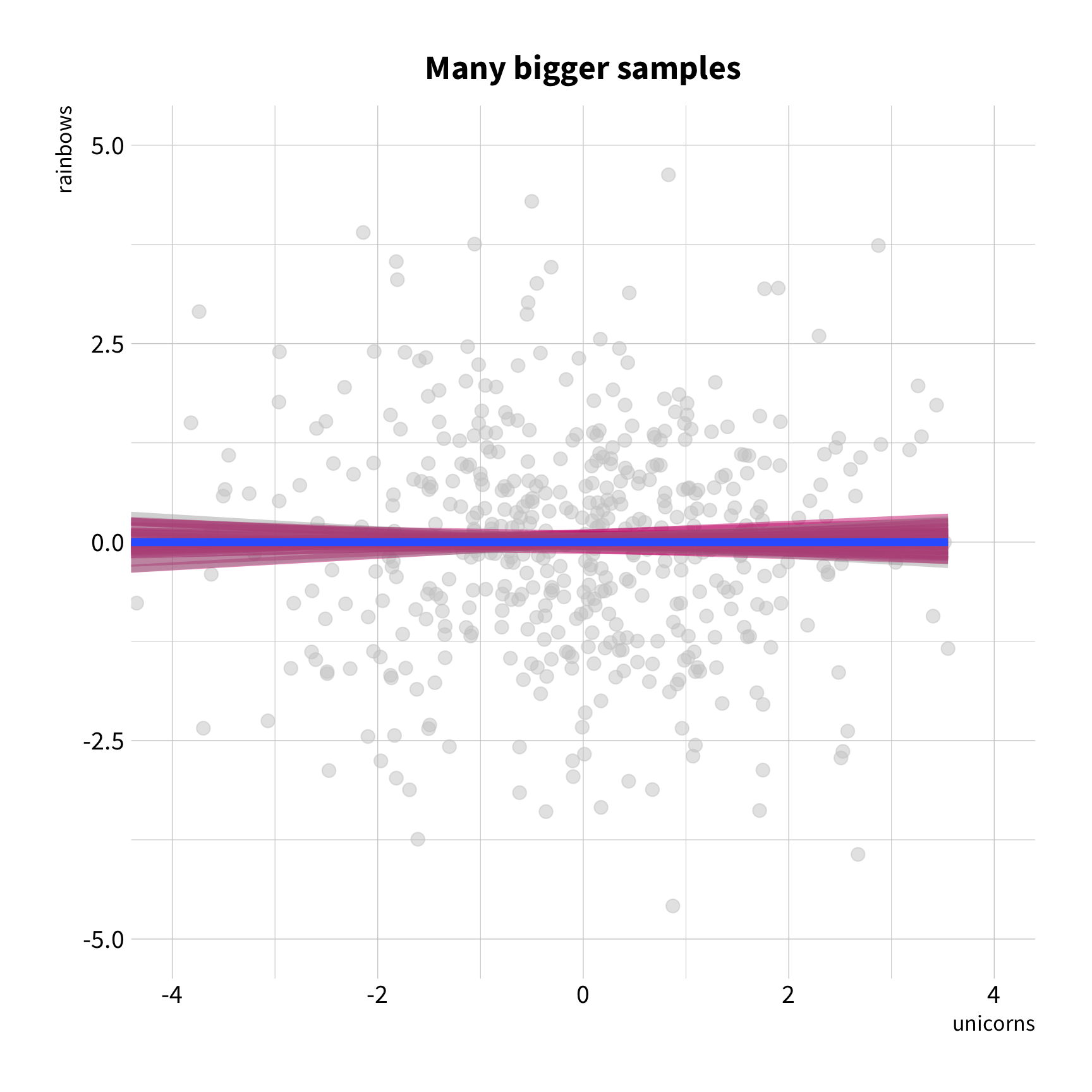
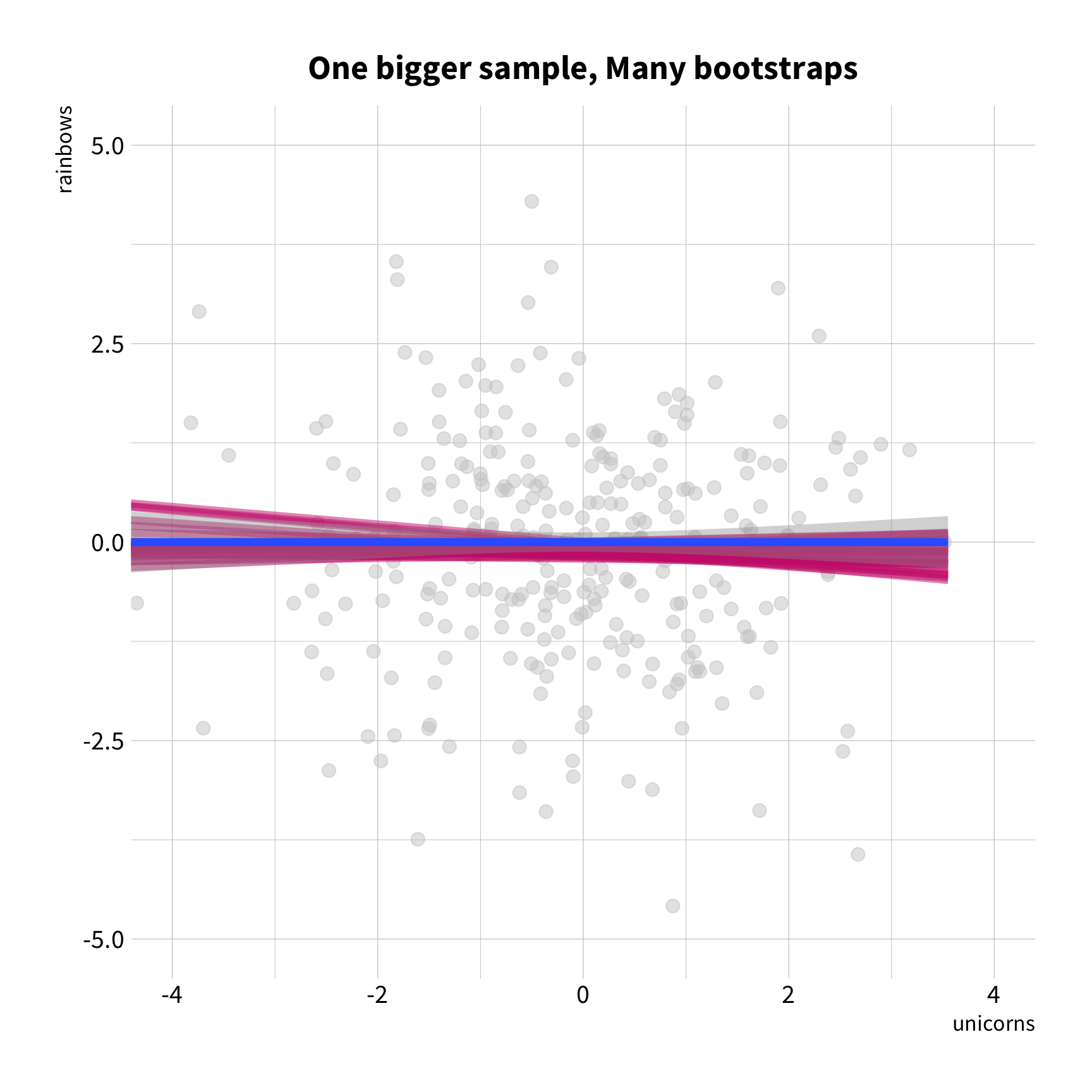
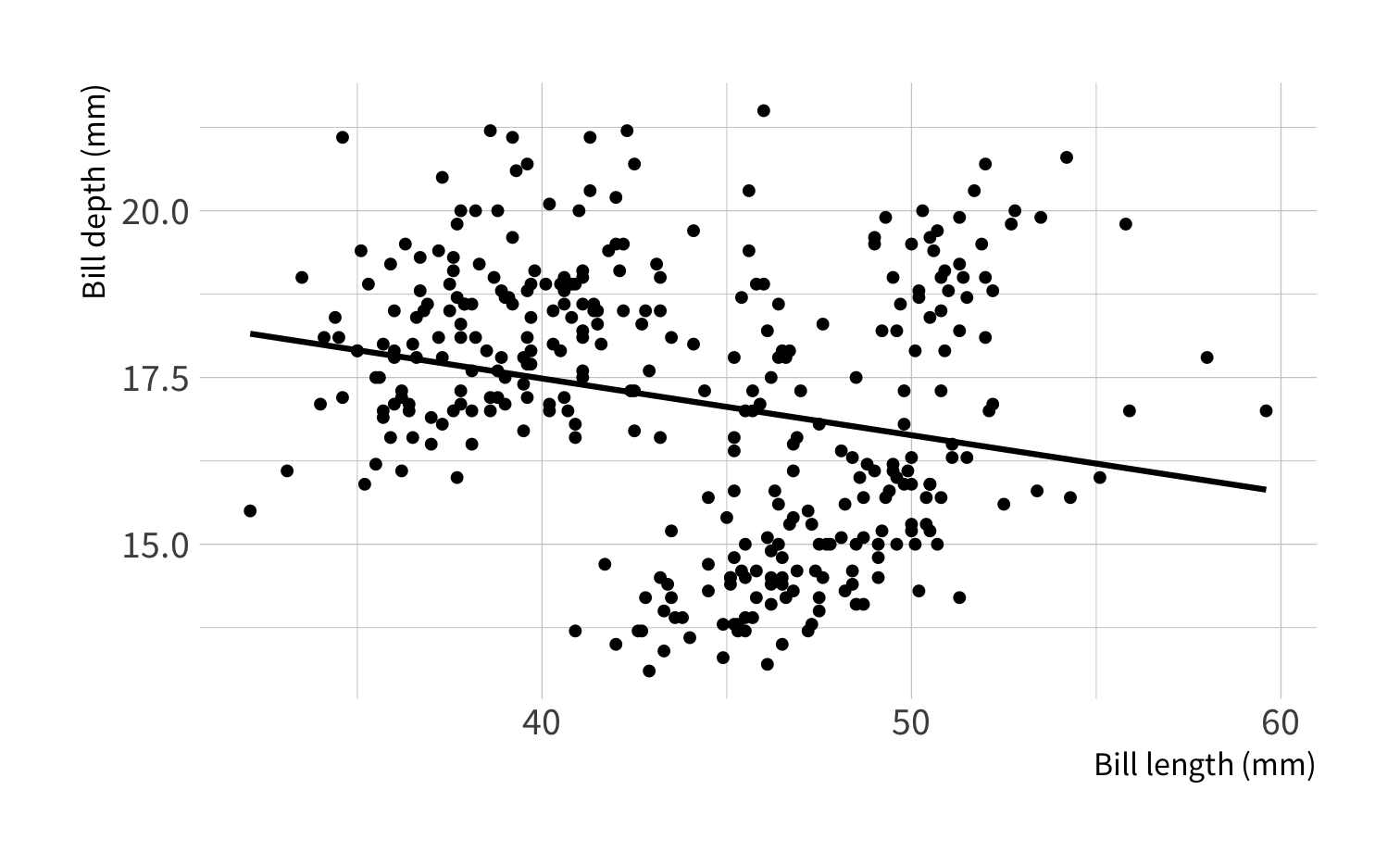
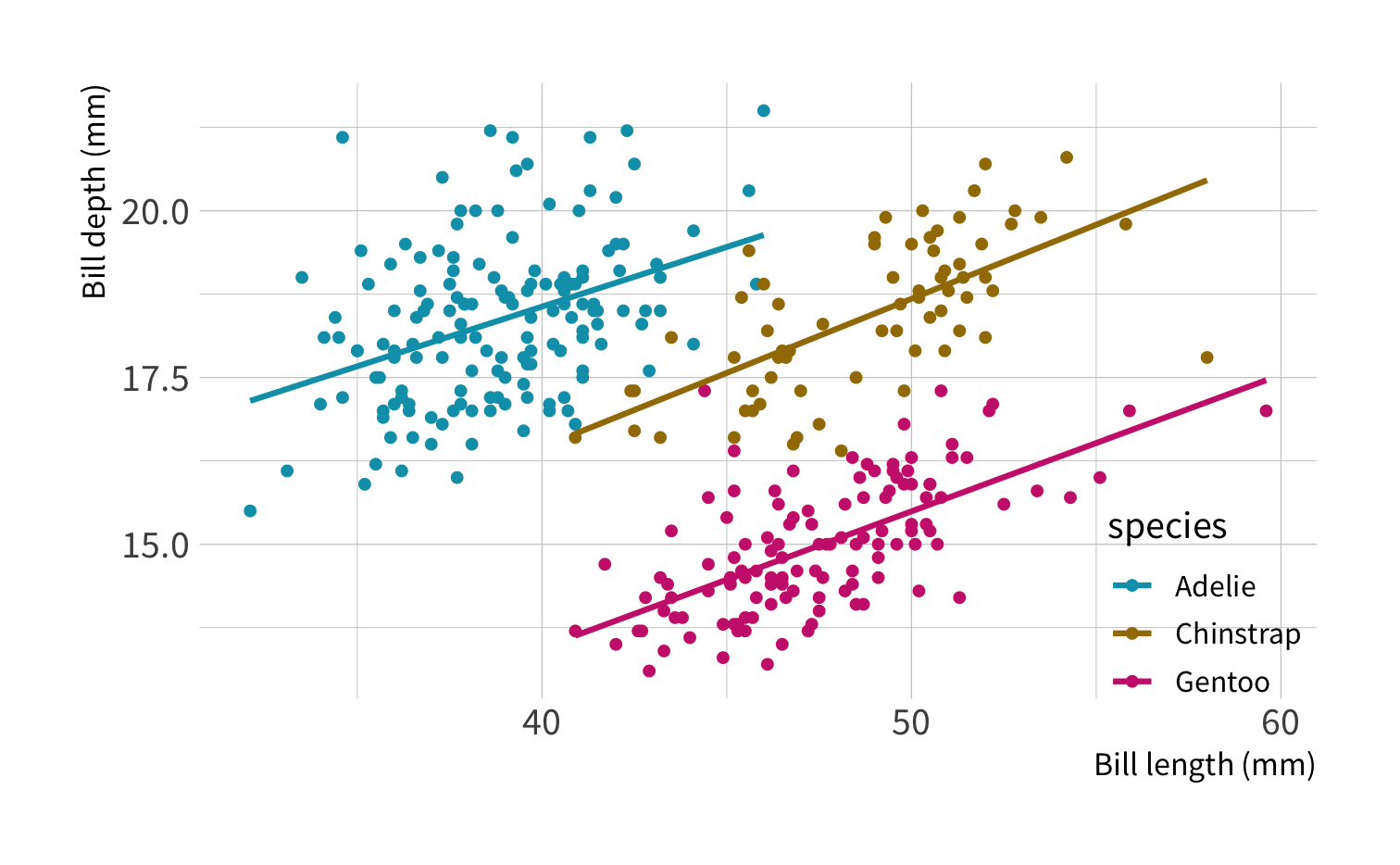
What is the correlation between bill length and bill depth?

library(palmerpenguins)
penguins
#> # A tibble: 344 x 8
#>    species island    bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
#>    <fct>   <fct>              <dbl>         <dbl>             <int>       <int>
#>  1 Adelie  Torgersen           39.1          18.7               181        3750
#>  2 Adelie  Torgersen           39.5          17.4               186        3800
#>  3 Adelie  Torgersen           40.3          18                 195        3250
#>  4 Adelie  Torgersen           NA            NA                  NA          NA
#>  5 Adelie  Torgersen           36.7          19.3               193        3450
#>  6 Adelie  Torgersen           39.3          20.6               190        3650
#>  7 Adelie  Torgersen           38.9          17.8               181        3625
#>  8 Adelie  Torgersen           39.2          19.6               195        4675
#>  9 Adelie  Torgersen           34.1          18.1               193        3475
#> 10 Adelie  Torgersen           42            20.2               190        4250
#> # … with 334 more rows, and 2 more variables: sex <fct>, year <int>

Artwork by @allison_horst

`bootstraps()`

Create bootstrap samples from a data set.

set.seed(100) # Important!
penguin_boot <- bootstraps(penguins, times = 25)

Your turn 1

Use bootstraps() to create 100 bootstrap samples of the penguins data.

Save the bootstrap samples as penguin_boot.

Keep set.seed(100)!

02:00

set.seed(100)
penguin_boot <- bootstraps(penguins, times = 100)
penguin_boot
#> # Bootstrap sampling 
#> # A tibble: 100 x 2
#>    splits            id          
#>    <list>            <chr>       
#>  1 <split [344/134]> Bootstrap001
#>  2 <split [344/126]> Bootstrap002
#>  3 <split [344/124]> Bootstrap003
#>  4 <split [344/129]> Bootstrap004
#>  5 <split [344/127]> Bootstrap005
#>  6 <split [344/124]> Bootstrap006
#>  7 <split [344/127]> Bootstrap007
#>  8 <split [344/125]> Bootstrap008
#>  9 <split [344/128]> Bootstrap009
#> 10 <split [344/123]> Bootstrap010
#> # … with 90 more rows

What is a <list>?

penguin_boot
#> # Bootstrap sampling 
#> # A tibble: 100 x 2
#>    splits            id          
#>    <list>            <chr>       
#>  1 <split [344/134]> Bootstrap001
#>  2 <split [344/126]> Bootstrap002
#>  3 <split [344/124]> Bootstrap003
#>  4 <split [344/129]> Bootstrap004
#>  5 <split [344/127]> Bootstrap005
#>  6 <split [344/124]> Bootstrap006
#>  7 <split [344/127]> Bootstrap007
#>  8 <split [344/125]> Bootstrap008
#>  9 <split [344/128]> Bootstrap009
#> 10 <split [344/123]> Bootstrap010
#> # … with 90 more rows

penguin_boot$splits[[1]] #> #> <344/134/344>

Anatomy of a split

<344/134/344>

Anatomy of a split

<344/134/344>

<344/134/344> >>> Size of resample (analysis set)

Anatomy of a split

<344/134/344>

<344/134/344> >>> Size of resample (analysis set)

<344/134/344> >>> Size of holdout/unused data (assessment set)

Anatomy of a split

<344/134/344>

<344/134/344> >>> Size of resample (analysis set)

<344/134/344> >>> Size of holdout/unused data (assessment set)

<344/134/344> >>> Total size of data set

Split databoot1 <- penguin_boot$splits[[1]]
boot1
#> <Analysis/Assess/Total>
#> <344/134/344>

Split databoot1 <- penguin_boot$splits[[1]]
boot1
#> <Analysis/Assess/Total>
#> <344/134/344>

analysis()analysis(boot1)
#> # A tibble: 344 x 8
#>    species   island    bill_length_mm bill_depth_mm flipper_length_… body_mass_g
#>    <fct>     <fct>              <dbl>         <dbl>            <int>       <int>
#>  1 Gentoo    Biscoe              45.2          15.8              215        5300
#>  2 Adelie    Biscoe              45.6          20.3              191        4600
#>  3 Gentoo    Biscoe              50.1          15                225        5000
#>  4 Adelie    Torgersen           NA            NA                 NA          NA
#>  5 Chinstrap Dream               49.7          18.6              195        3600
#>  6 Chinstrap Dream               49.8          17.3              198        3675
#>  7 Adelie    Dream               40.3          18.5              196        4350
#>  8 Adelie    Torgersen           38.9          17.8              181        3625
#>  9 Gentoo    Biscoe              47.3          15.3              222        5250
#> 10 Chinstrap Dream               43.2          16.6              187        2900
#> # … with 334 more rows, and 2 more variables: sex <fct>, year <int>

Split databoot1 <- penguin_boot$splits[[1]]
boot1
#> <Analysis/Assess/Total>
#> <344/134/344>

analysis()analysis(boot1)
#> # A tibble: 344 x 8
#>    species   island    bill_length_mm bill_depth_mm flipper_length_… body_mass_g
#>    <fct>     <fct>              <dbl>         <dbl>            <int>       <int>
#>  1 Gentoo    Biscoe              45.2          15.8              215        5300
#>  2 Adelie    Biscoe              45.6          20.3              191        4600
#>  3 Gentoo    Biscoe              50.1          15                225        5000
#>  4 Adelie    Torgersen           NA            NA                 NA          NA
#>  5 Chinstrap Dream               49.7          18.6              195        3600
#>  6 Chinstrap Dream               49.8          17.3              198        3675
#>  7 Adelie    Dream               40.3          18.5              196        4350
#>  8 Adelie    Torgersen           38.9          17.8              181        3625
#>  9 Gentoo    Biscoe              47.3          15.3              222        5250
#> 10 Chinstrap Dream               43.2          16.6              187        2900
#> # … with 334 more rows, and 2 more variables: sex <fct>, year <int>

assessment()assessment(boot1)
#> # A tibble: 134 x 8
#>    species island    bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
#>    <fct>   <fct>              <dbl>         <dbl>             <int>       <int>
#>  1 Adelie  Torgersen           36.7          19.3               193        3450
#>  2 Adelie  Torgersen           39.3          20.6               190        3650
#>  3 Adelie  Torgersen           39.2          19.6               195        4675
#>  4 Adelie  Torgersen           34.1          18.1               193        3475
#>  5 Adelie  Torgersen           42            20.2               190        4250
#>  6 Adelie  Torgersen           38.7          19                 195        3450
#>  7 Adelie  Torgersen           42.5          20.7               197        4500
#>  8 Adelie  Biscoe              37.7          18.7               180        3600
#>  9 Adelie  Biscoe              38.2          18.1               185        3950
#> 10 Adelie  Biscoe              40.6          18.6               183        3550
#> # … with 124 more rows, and 2 more variables: sex <fct>, year <int>

Pop quiz!

Why is the assessment set a different size for each bootstrap resample?

#> # Bootstrap sampling 
#> # A tibble: 100 x 2
#>    splits            id          
#>    <list>            <chr>       
#>  1 <split [344/134]> Bootstrap001
#>  2 <split [344/126]> Bootstrap002
#>  3 <split [344/124]> Bootstrap003
#>  4 <split [344/129]> Bootstrap004
#>  5 <split [344/127]> Bootstrap005
#>  6 <split [344/124]> Bootstrap006
#>  7 <split [344/127]> Bootstrap007
#>  8 <split [344/125]> Bootstrap008
#>  9 <split [344/128]> Bootstrap009
#> 10 <split [344/123]> Bootstrap010
#> # … with 90 more rows

01:00

Correlation

To estimate the correlation for a data set, use the cor() function.

boot1 <- penguin_boot$splits[[1]]
boot_sample <- analysis(boot1)
cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm)
#> [1] NA

Correlation

To estimate the correlation for a data set, use the cor() function.

boot1 <- penguin_boot$splits[[1]]
boot_sample <- analysis(boot1)
cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm)
#> [1] NA

cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm,
    use = "complete.obs")
#> [1] -0.1249339

Your turn 2

Complete the code to calculate the correlation for the fifth bootstrap sample.

boot5 <- boot_sample <- (boot5) cor(boot_sample$ , boot_sample$ , use = )

04:00

boot5 <- penguin_boot$splits[[5]]
boot_sample <- analysis(boot5)
cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm,
    use = "complete.obs")
#> [1] -0.2450851

Automation

(Applied) Data Science

`map()` and friends

Applies a function to every element of a list.

map(.x, .f, ...)

`map()` and friends

Applies a function to every element of a list.

map(.x, .f, ...)

What output do you expect?

map_chr(), map_dbl(), map_int(), map_lgl(), map_df(), or the general map()

Building our `map()`

map(penguin_boot$splits, .f)

Custom functions

We need a function that:

1. Takes in a split

2. Pull out the analysis set

3. Calculates the correlation of the analysis set

Step 1: Create the code

Use our code from earlier

boot_sample <- analysis(split) cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm, use = "complete.obs")

Step 1: Create the code

Use our code from earlier

boot_sample <- analysis(split) cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm, use = "complete.obs")

Step 2: Wrap inside of `function()`

The function() function defines a new function

penguin_cor <- function(split) { boot_sample <- analysis(split) cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm, use = "complete.obs") }

Step 2: Wrap inside of `function()`

The code gets wrapped inside of the curly braces

penguin_cor <- function(split) { boot_sample <- analysis(split) cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm, use = "complete.obs") }

Step 2: Wrap inside of `function()`

Give the function a name

penguin_cor <- function(split) { boot_sample <- analysis(split) cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm, use = "complete.obs") }

Step 3: Verify it works as expected

boot1 <- penguin_boot$splits[[1]]
boot1_sample <- analysis(boot1)
cor(boot1_sample$bill_length_mm, boot1_sample$bill_depth_mm,
    use = "complete.obs")
#> [1] -0.1249339

Step 3: Verify it works as expected

boot1 <- penguin_boot$splits[[1]]
boot1_sample <- analysis(boot1)
cor(boot1_sample$bill_length_mm, boot1_sample$bill_depth_mm,
    use = "complete.obs")
#> [1] -0.1249339

penguin_cor(boot1)
#> [1] -0.1249339

Building our `map()`

map(penguin_boot$splits, penguin_cor)
#> [[1]]
#> [1] -0.1249339
#> 
#> [[2]]
#> [1] -0.2541791
#> 
#> [[3]]
#> [1] -0.1991897
#> 
#> [[4]]
#> [1] -0.2478776
#> 
#> [[5]]
#> [1] -0.2450851
#> 
#> [[6]]
#> [1] -0.2792748
#> 
#> [[7]]
#> [1] -0.2776204
#> 
#> [[8]]
#> [1] -0.2045329
#> 
#> [[9]]
#> [1] -0.2431401
#> 
#> [[10]]
#> [1] -0.2745247
#> 
#> [[11]]
#> [1] -0.3171123
#> 
#> [[12]]
#> [1] -0.2259223
#> 
#> [[13]]
#> [1] -0.2044941
#> 
#> [[14]]
#> [1] -0.1027711
#> 
#> [[15]]
#> [1] -0.2506249
#> 
#> [[16]]
#> [1] -0.225205
#> 
#> [[17]]
#> [1] -0.2336472
#> 
#> [[18]]
#> [1] -0.2458328
#> 
#> [[19]]
#> [1] -0.2302427
#> 
#> [[20]]
#> [1] -0.2119384
#> 
#> [[21]]
#> [1] -0.1615742
#> 
#> [[22]]
#> [1] -0.308794
#> 
#> [[23]]
#> [1] -0.08155008
#> 
#> [[24]]
#> [1] -0.2548912
#> 
#> [[25]]
#> [1] -0.244613
#> 
#> [[26]]
#> [1] -0.2485528
#> 
#> [[27]]
#> [1] -0.23714
#> 
#> [[28]]
#> [1] -0.2015473
#> 
#> [[29]]
#> [1] -0.2691933
#> 
#> [[30]]
#> [1] -0.2407836
#> 
#> [[31]]
#> [1] -0.2307748
#> 
#> [[32]]
#> [1] -0.254897
#> 
#> [[33]]
#> [1] -0.2027794
#> 
#> [[34]]
#> [1] -0.2285699
#> 
#> [[35]]
#> [1] -0.164203
#> 
#> [[36]]
#> [1] -0.2912028
#> 
#> [[37]]
#> [1] -0.2936487
#> 
#> [[38]]
#> [1] -0.2951136
#> 
#> [[39]]
#> [1] -0.1986556
#> 
#> [[40]]
#> [1] -0.2981575
#> 
#> [[41]]
#> [1] -0.2325189
#> 
#> [[42]]
#> [1] -0.3074985
#> 
#> [[43]]
#> [1] -0.2465553
#> 
#> [[44]]
#> [1] -0.1778199
#> 
#> [[45]]
#> [1] -0.253044
#> 
#> [[46]]
#> [1] -0.2090783
#> 
#> [[47]]
#> [1] -0.2371913
#> 
#> [[48]]
#> [1] -0.2546507
#> 
#> [[49]]
#> [1] -0.2835118
#> 
#> [[50]]
#> [1] -0.2080868
#> 
#> [[51]]
#> [1] -0.2627895
#> 
#> [[52]]
#> [1] -0.198087
#> 
#> [[53]]
#> [1] -0.214096
#> 
#> [[54]]
#> [1] -0.2348333
#> 
#> [[55]]
#> [1] -0.2161979
#> 
#> [[56]]
#> [1] -0.2515138
#> 
#> [[57]]
#> [1] -0.1813075
#> 
#> [[58]]
#> [1] -0.2178123
#> 
#> [[59]]
#> [1] -0.3049228
#> 
#> [[60]]
#> [1] -0.2239921
#> 
#> [[61]]
#> [1] -0.1970032
#> 
#> [[62]]
#> [1] -0.2332788
#> 
#> [[63]]
#> [1] -0.2436859
#> 
#> [[64]]
#> [1] -0.2748855
#> 
#> [[65]]
#> [1] -0.2315254
#> 
#> [[66]]
#> [1] -0.2064697
#> 
#> [[67]]
#> [1] -0.3404718
#> 
#> [[68]]
#> [1] -0.1539548
#> 
#> [[69]]
#> [1] -0.3189776
#> 
#> [[70]]
#> [1] -0.2708725
#> 
#> [[71]]
#> [1] -0.2243308
#> 
#> [[72]]
#> [1] -0.2800821
#> 
#> [[73]]
#> [1] -0.2363227
#> 
#> [[74]]
#> [1] -0.2387688
#> 
#> [[75]]
#> [1] -0.2112919
#> 
#> [[76]]
#> [1] -0.2377676
#> 
#> [[77]]
#> [1] -0.1885858
#> 
#> [[78]]
#> [1] -0.2639419
#> 
#> [[79]]
#> [1] -0.3930653
#> 
#> [[80]]
#> [1] -0.2140946
#> 
#> [[81]]
#> [1] -0.1766409
#> 
#> [[82]]
#> [1] -0.1848252
#> 
#> [[83]]
#> [1] -0.1868983
#> 
#> [[84]]
#> [1] -0.3049031
#> 
#> [[85]]
#> [1] -0.2336121
#> 
#> [[86]]
#> [1] -0.2459616
#> 
#> [[87]]
#> [1] -0.2671155
#> 
#> [[88]]
#> [1] -0.3290882
#> 
#> [[89]]
#> [1] -0.2258902
#> 
#> [[90]]
#> [1] -0.2425831
#> 
#> [[91]]
#> [1] -0.2154876
#> 
#> [[92]]
#> [1] -0.2990681
#> 
#> [[93]]
#> [1] -0.1735009
#> 
#> [[94]]
#> [1] -0.2217043
#> 
#> [[95]]
#> [1] -0.2614308
#> 
#> [[96]]
#> [1] -0.2955381
#> 
#> [[97]]
#> [1] -0.2524951
#> 
#> [[98]]
#> [1] -0.2194297
#> 
#> [[99]]
#> [1] -0.2214609
#> 
#> [[100]]
#> [1] -0.1783059

`map()` + `mutate()`

penguin_boot %>%
  mutate(corr = map(splits, penguin_cor))
#> # Bootstrap sampling 
#> # A tibble: 100 x 3
#>    splits            id           corr     
#>    <list>            <chr>        <list>   
#>  1 <split [344/134]> Bootstrap001 <dbl [1]>
#>  2 <split [344/126]> Bootstrap002 <dbl [1]>
#>  3 <split [344/124]> Bootstrap003 <dbl [1]>
#>  4 <split [344/129]> Bootstrap004 <dbl [1]>
#>  5 <split [344/127]> Bootstrap005 <dbl [1]>
#>  6 <split [344/124]> Bootstrap006 <dbl [1]>
#>  7 <split [344/127]> Bootstrap007 <dbl [1]>
#>  8 <split [344/125]> Bootstrap008 <dbl [1]>
#>  9 <split [344/128]> Bootstrap009 <dbl [1]>
#> 10 <split [344/123]> Bootstrap010 <dbl [1]>
#> # … with 90 more rows

What's wrong with this? What could be improved?

`map_dbl()` + `mutate()`

penguin_boot %>%
  mutate(corr = map_dbl(splits, penguin_cor))
#> # Bootstrap sampling 
#> # A tibble: 100 x 3
#>    splits            id             corr
#>    <list>            <chr>         <dbl>
#>  1 <split [344/134]> Bootstrap001 -0.125
#>  2 <split [344/126]> Bootstrap002 -0.254
#>  3 <split [344/124]> Bootstrap003 -0.199
#>  4 <split [344/129]> Bootstrap004 -0.248
#>  5 <split [344/127]> Bootstrap005 -0.245
#>  6 <split [344/124]> Bootstrap006 -0.279
#>  7 <split [344/127]> Bootstrap007 -0.278
#>  8 <split [344/125]> Bootstrap008 -0.205
#>  9 <split [344/128]> Bootstrap009 -0.243
#> 10 <split [344/123]> Bootstrap010 -0.275
#> # … with 90 more rows

Your turn 3

Use the mapping functions and mutate() to calculate the correlation between bill length and bill depth.

1. Write a function to calculate the correlation from the analysis set of a split.

2. Apply that function to every bootstrap sample using mutate() and mapping function.

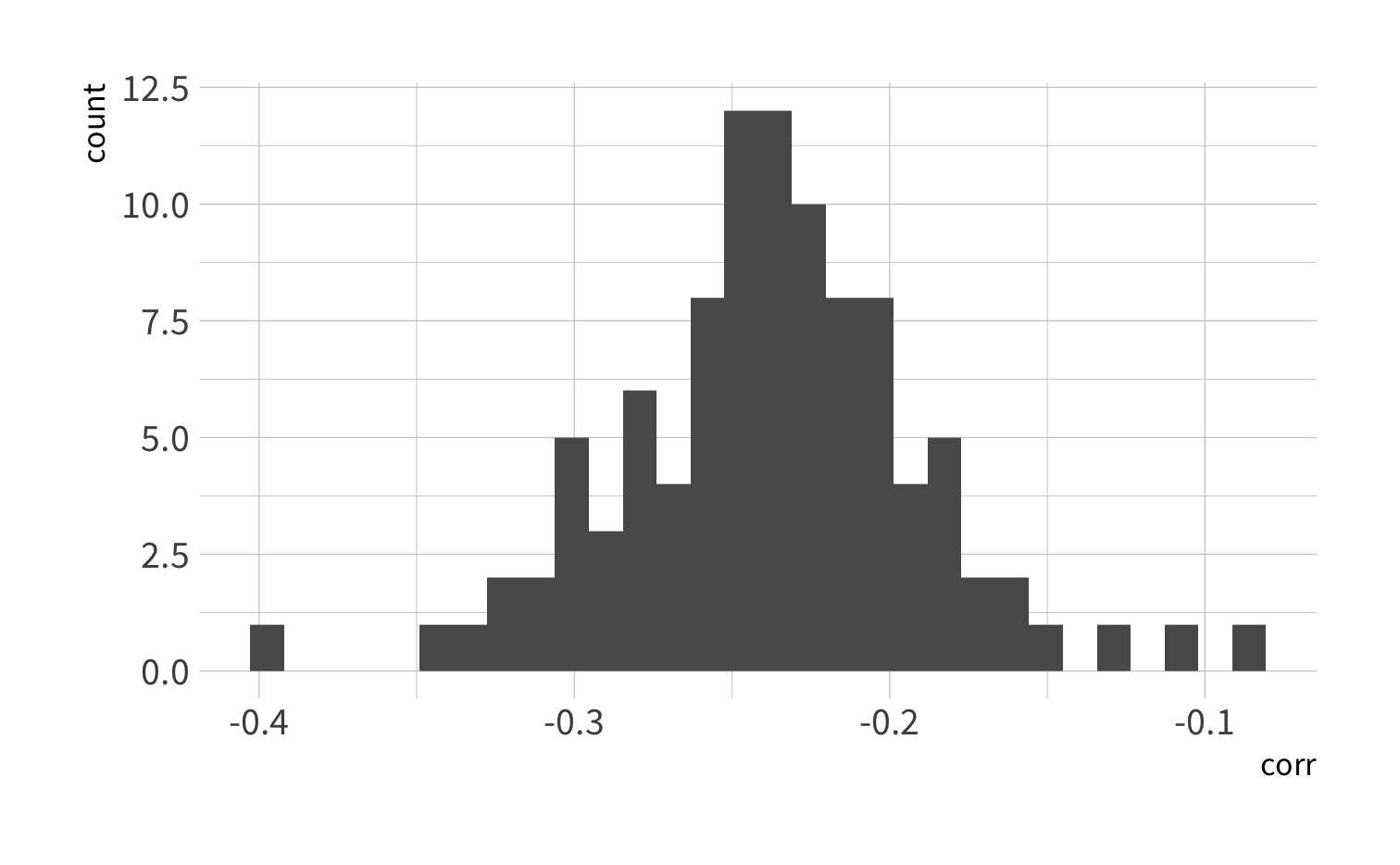
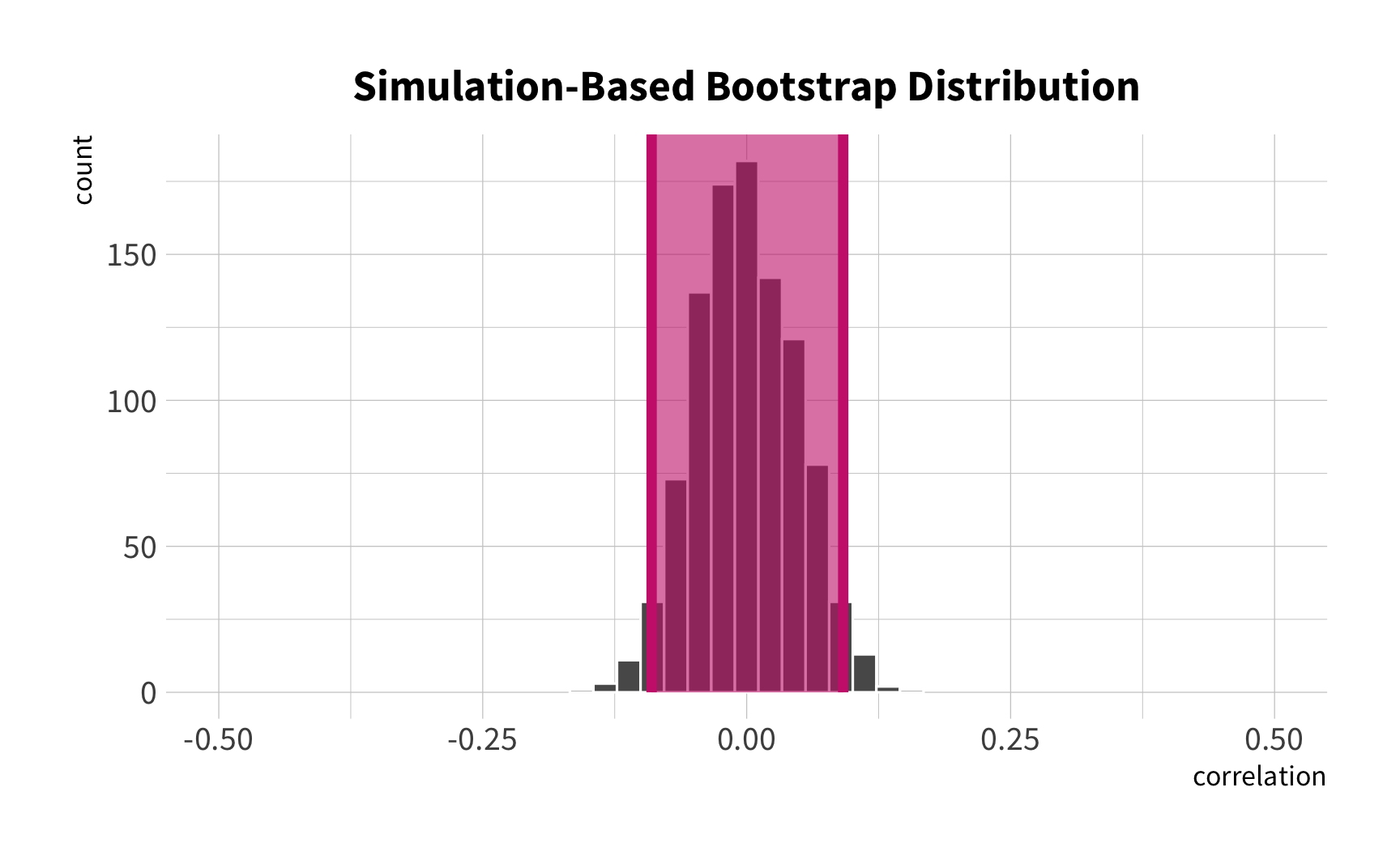
3. Make a histogram of the bootstrapped correlations.

05:00

penguin_cor <- function(split) {
  boot_sample <- analysis(split)
  cor(boot_sample$bill_length_mm, boot_sample$bill_depth_mm,
      use = "complete.obs")
}

penguin_boot %>%
  mutate(corr = map_dbl(splits, penguin_cor)) %>%
  ggplot(mapping = aes(x = corr)) +
  geom_histogram()

Bootstrap summaries

penguin_boot %>%
  mutate(corr = map_dbl(splits, penguin_cor)) %>%
  summarize(avg_corr = mean(corr))
#> # A tibble: 1 x 1
#>   avg_corr
#>      <dbl>
#> 1   -0.237

Bootstrap summaries

penguin_boot %>%
  mutate(corr = map_dbl(splits, penguin_cor)) %>%
  summarize(interval_95 = quantile(corr, probs = c(0.025, 0.975)),
            quantile = c(0.025, 0.975))
#> # A tibble: 2 x 2
#>   interval_95 quantile
#>         <dbl>    <dbl>
#> 1      -0.324    0.025
#> 2      -0.139    0.975

r = −.24

Adelie r = .39; Chinstrap r = .65; Gentoo r = .64

Cross-validation

Your turn 4

1. Use initial_split() to create a training and testing set of the penguins data.

2. Write a parsnip specification to fit a linear model that uses flipper length to predict bill length.

3. Use the testing data to calculate the RMSE.

06:00

penguin_split <- initial_split(penguins)
penguin_train <- training(penguin_split)
penguin_test <- testing(penguin_split)
lm_spec <- linear_reg() %>%
  set_engine("lm") %>%
  set_mode("regression")
lm_model <- fit(lm_spec,
                bill_length_mm ~ flipper_length_mm,
                data = penguin_train)
lm_preds <- predict(lm_model, new_data = penguin_test) %>%
  mutate(.truth = penguin_test$bill_length_mm)
rmse(lm_preds, truth = .truth, estimate = .pred)
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        4.69

Your turn 5

What would happen if you repeated this process? Would you get the same answers?

Rerun the code chunk from the last exercise. Do you get the same answer?

02:00

#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        3.66
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        3.91
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        4.61

#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        3.66
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        3.91
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        4.61
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        4.16
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        4.01
#> # A tibble: 1 x 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        3.88

Pop quiz!

Why is the new estimate different?

Mean RMSE

rmses %>% enframe(name = "rmse")
#> # A tibble: 10 x 2
#>     rmse value
#>    <int> <dbl>
#>  1     1  3.72
#>  2     2  3.65
#>  3     3  4.70
#>  4     4  4.31
#>  5     5  3.82
#>  6     6  4.39
#>  7     7  4.08
#>  8     8  4.85
#>  9     9  4.57
#> 10    10  4.08
mean(rmses)
#> [1] 4.216917

Consider

Which do you think is more accurate, the best result or the mean of the results? Why?

There has to be a better way...

rmses <- vector(length = 10, mode = "double")
for (i in seq_along(rmses)) {
  new_split <- initial_split(penguins)
  penguin_train <- training(new_split)
  penguin_test <- testing(new_split)
  lm_model <- fit(lm_spec,
                  bill_length_mm ~ flipper_length_mm,
                  data = penguin_train)
  lm_preds <- predict(lm_model,
                      new_data = penguin_test) %>%
    mutate(.truth = penguin_test$bill_length_mm)
  rmses[i] <- rmse(lm_preds, truth = .truth, estimate = .pred) %>%
    pull(.estimate)
}

V-fold cross-validation

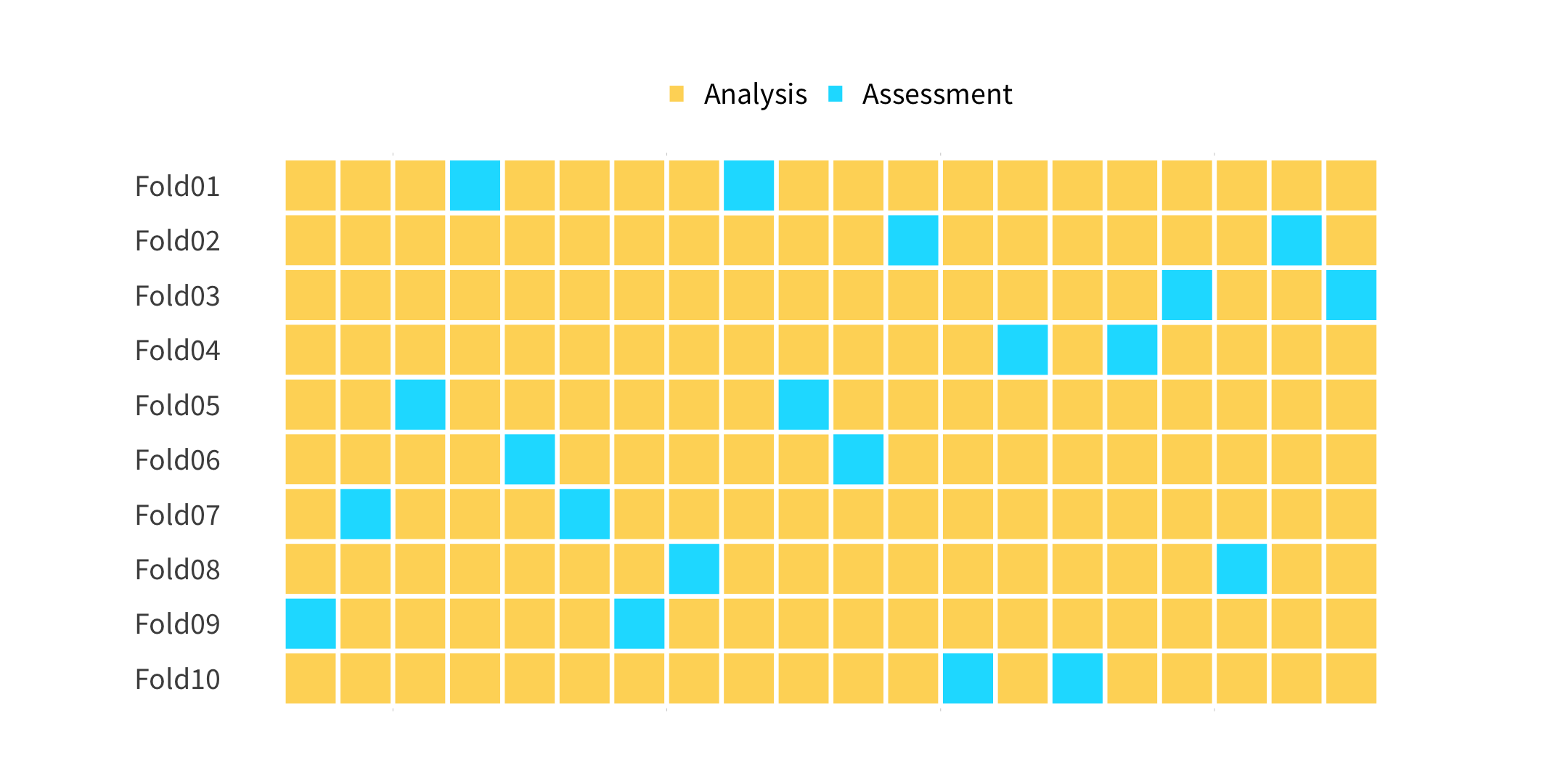
vfold_cv(data, v = 10, ...)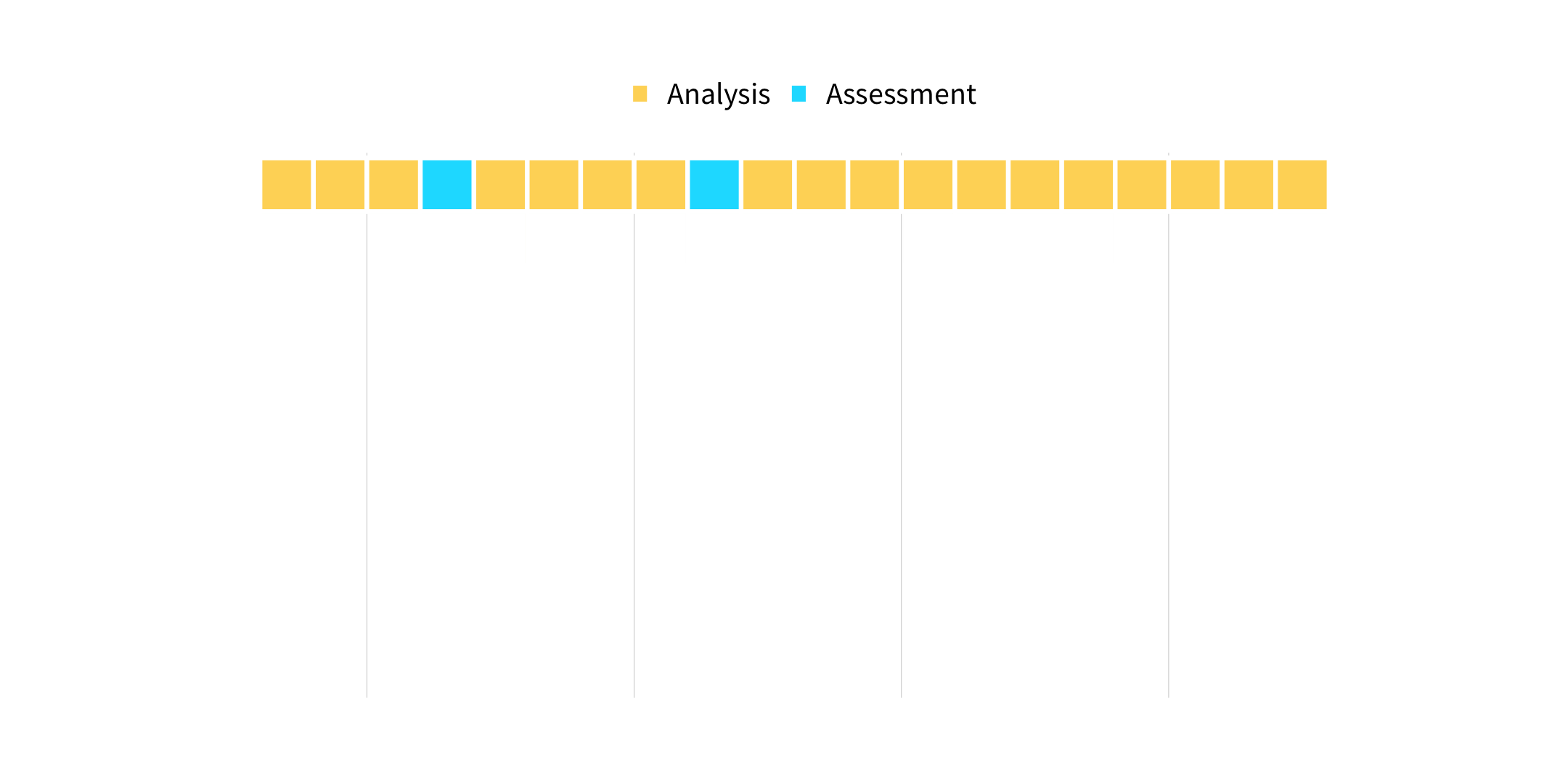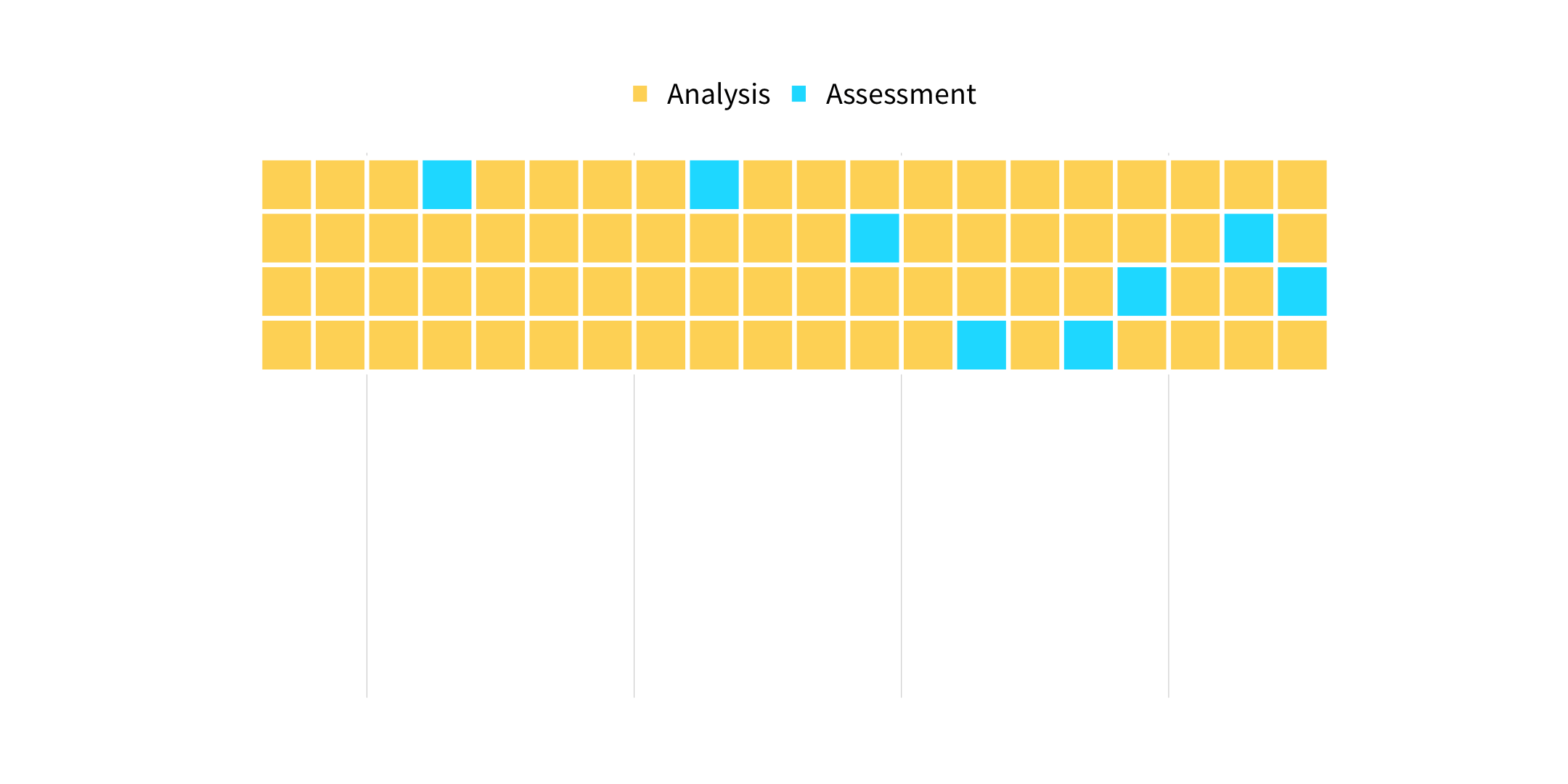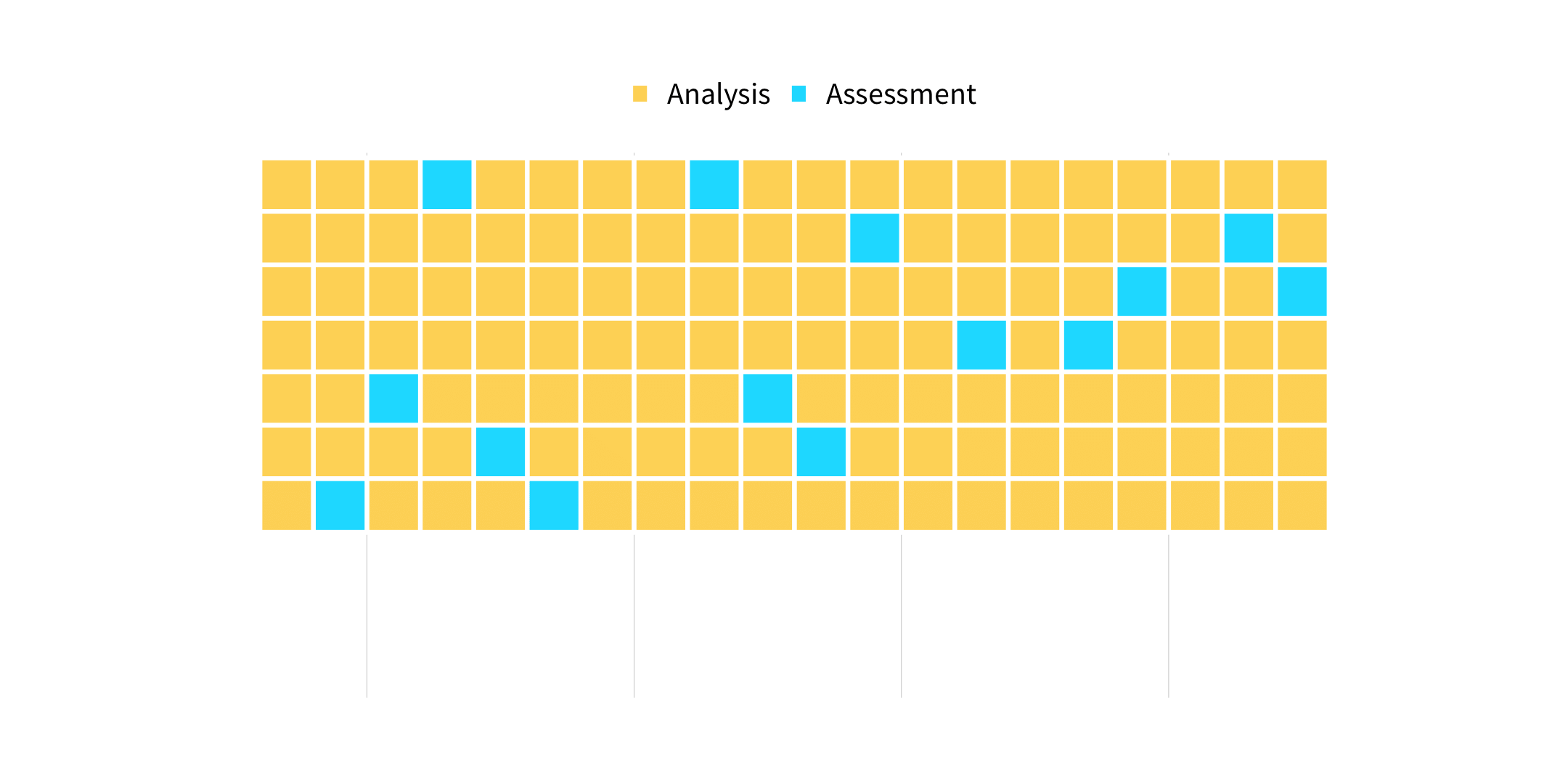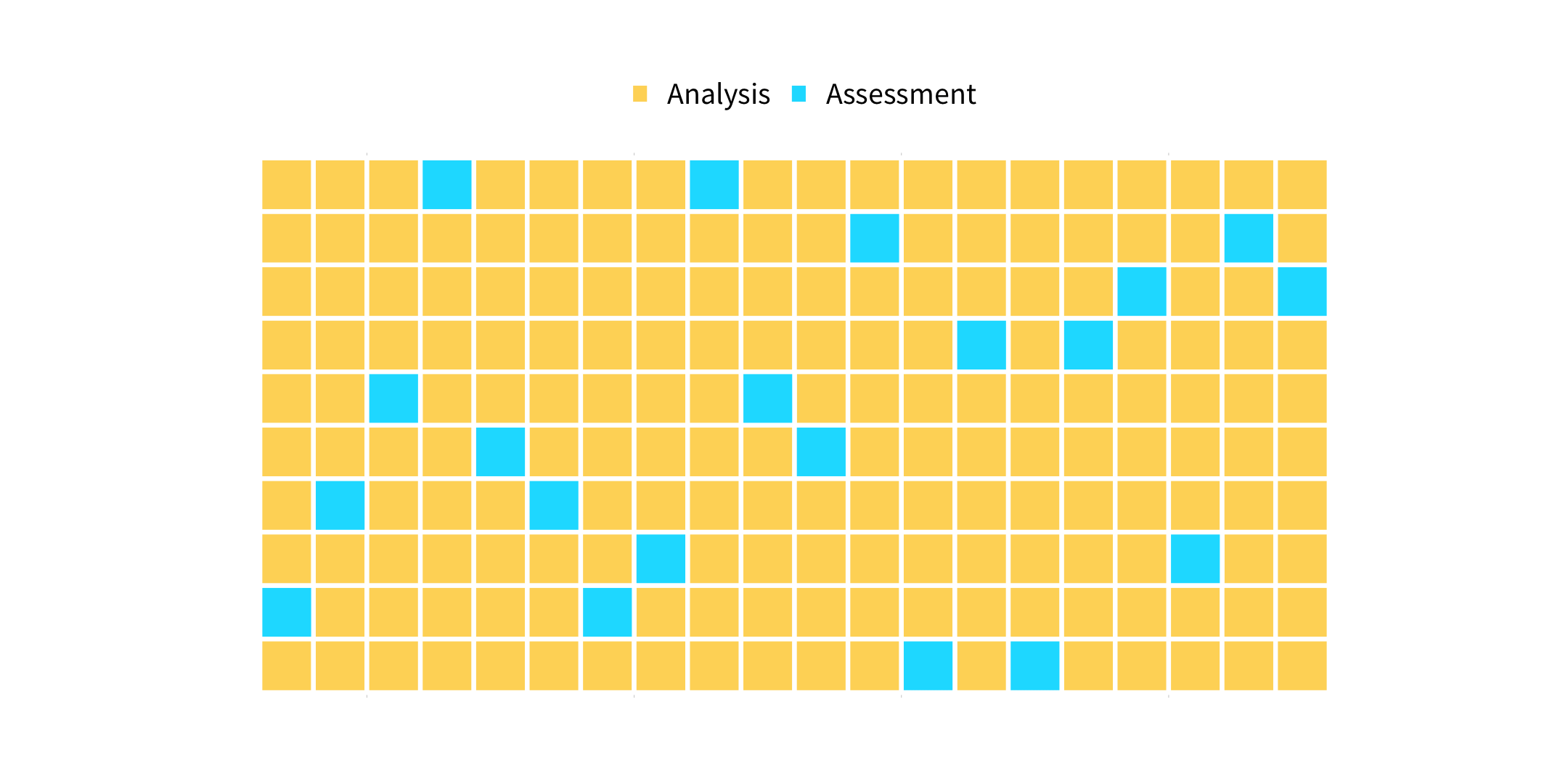

Guess

How many times does an observation/row appear in the assessment set?

Pop quiz!

If we use 10 folds, what percent of our data will end up in the training set and what percent in the testing set for each fold?

01:00

Pop quiz!

If we use 10 folds, what percent of our data will end up in the training set and what percent in the testing set for each fold?

90% training

10% testing

Your turn 6

Run the code below. What does it return?

set.seed(100)
cv_folds <- vfold_cv(penguins, v = 10, strata = species)
cv_folds

01:00

cv_folds
#> #  10-fold cross-validation using stratification 
#> # A tibble: 10 x 2
#>    splits           id    
#>    <list>           <chr> 
#>  1 <split [308/36]> Fold01
#>  2 <split [308/36]> Fold02
#>  3 <split [309/35]> Fold03
#>  4 <split [309/35]> Fold04
#>  5 <split [310/34]> Fold05
#>  6 <split [310/34]> Fold06
#>  7 <split [310/34]> Fold07
#>  8 <split [310/34]> Fold08
#>  9 <split [311/33]> Fold09
#> 10 <split [311/33]> Fold10

How does this help us?

`fit_resamples()`

Trains and tests a model with cross-validation.

fit_resamples(lm_spec,
              bill_length_mm ~ flipper_length_mm,
              resamples = cv_folds)

fit_resamples(lm_spec,
              bill_length_mm ~ flipper_length_mm,
              resamples = cv_folds)
#> # Resampling results
#> # 10-fold cross-validation using stratification 
#> # A tibble: 10 x 4
#>    splits           id     .metrics             .notes              
#>    <list>           <chr>  <list>               <list>              
#>  1 <split [308/36]> Fold01 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  2 <split [308/36]> Fold02 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  3 <split [309/35]> Fold03 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  4 <split [309/35]> Fold04 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  5 <split [310/34]> Fold05 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  6 <split [310/34]> Fold06 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  7 <split [310/34]> Fold07 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  8 <split [310/34]> Fold08 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#>  9 <split [311/33]> Fold09 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>
#> 10 <split [311/33]> Fold10 <tibble[,4] [2 × 4]> <tibble[,1] [0 × 1]>

`collect_metrics()`

Collect metrics from a cross-validation.

cv_results %>%
  collect_metrics()
#> # A tibble: 2 x 6
#>   .metric .estimator  mean     n std_err .config             
#>   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
#> 1 rmse    standard   4.11     10  0.158  Preprocessor1_Model1
#> 2 rsq     standard   0.444    10  0.0422 Preprocessor1_Model1

`collect_metrics()`

Collect metrics from a cross-validation.

cv_results %>%
  collect_metrics()
#> # A tibble: 2 x 6
#>   .metric .estimator  mean     n std_err .config             
#>   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
#> 1 rmse    standard   4.11     10  0.158  Preprocessor1_Model1
#> 2 rsq     standard   0.444    10  0.0422 Preprocessor1_Model1

cv_results %>%
  collect_metrics(summarize = FALSE)
#> # A tibble: 20 x 5
#>    id     .metric .estimator .estimate .config             
#>    <chr>  <chr>   <chr>          <dbl> <chr>               
#>  1 Fold01 rmse    standard       3.77  Preprocessor1_Model1
#>  2 Fold01 rsq     standard       0.451 Preprocessor1_Model1
#>  3 Fold02 rmse    standard       4.43  Preprocessor1_Model1
#>  4 Fold02 rsq     standard       0.295 Preprocessor1_Model1
#>  5 Fold03 rmse    standard       3.83  Preprocessor1_Model1
#>  6 Fold03 rsq     standard       0.315 Preprocessor1_Model1
#>  7 Fold04 rmse    standard       4.16  Preprocessor1_Model1
#>  8 Fold04 rsq     standard       0.496 Preprocessor1_Model1
#>  9 Fold05 rmse    standard       4.16  Preprocessor1_Model1
#> 10 Fold05 rsq     standard       0.560 Preprocessor1_Model1
#> 11 Fold06 rmse    standard       5.11  Preprocessor1_Model1
#> 12 Fold06 rsq     standard       0.220 Preprocessor1_Model1
#> 13 Fold07 rmse    standard       4.24  Preprocessor1_Model1
#> 14 Fold07 rsq     standard       0.594 Preprocessor1_Model1
#> 15 Fold08 rmse    standard       4.45  Preprocessor1_Model1
#> 16 Fold08 rsq     standard       0.387 Preprocessor1_Model1
#> 17 Fold09 rmse    standard       3.56  Preprocessor1_Model1
#> 18 Fold09 rsq     standard       0.593 Preprocessor1_Model1
#> 19 Fold10 rmse    standard       3.39  Preprocessor1_Model1
#> 20 Fold10 rsq     standard       0.528 Preprocessor1_Model1

`metric_set()`

Specify which metrics you want to get back.

fit_resamples(lm_spec,
              bill_length_mm ~ flipper_length_mm,
              resamples = cv_folds,
              metrics = metric_set(rsq)) %>%
  collect_metrics()
#> # A tibble: 1 x 6
#>   .metric .estimator  mean     n std_err .config             
#>   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
#> 1 rsq     standard   0.444    10  0.0422 Preprocessor1_Model1

Your Turn 7

Modify the code below to estimate our model on each of the folds and calculate the average RMSE for our penguin model.

fit(lm_spec,
    bill_length_mm ~ flipper_length_mm,
    data = penguins)

03:00

fit_resamples(lm_spec,
              bill_length_mm ~ flipper_length_mm,
              resamples = cv_folds,
              metrics = metric_set(rmse)) %>%
  collect_metrics()
#> # A tibble: 1 x 6
#>   .metric .estimator  mean     n std_err .config             
#>   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
#> 1 rmse    standard    4.11    10   0.158 Preprocessor1_Model1

Comparing Models

Your Turn 8

Use fit_resamples() and cv_folds to estimate to models two predict bill length.

1. bill_length_mm ~ flipper_length_mm

2. bill_length_mm ~ species + sex

Compare the performance of each.

06:00

fit_resamples(lm_spec,
              bill_length_mm ~ flipper_length_mm,
              resamples = cv_folds) %>%
  collect_metrics()
#> # A tibble: 2 x 6
#>   .metric .estimator  mean     n std_err .config             
#>   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
#> 1 rmse    standard   4.11     10  0.158  Preprocessor1_Model1
#> 2 rsq     standard   0.444    10  0.0422 Preprocessor1_Model1
fit_resamples(lm_spec,
              bill_length_mm ~ species + sex,
              resamples = cv_folds) %>%
  collect_metrics()
#> # A tibble: 2 x 6
#>   .metric .estimator  mean     n std_err .config             
#>   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
#> 1 rmse    standard   2.33     10  0.118  Preprocessor1_Model1
#> 2 rsq     standard   0.833    10  0.0130 Preprocessor1_Model1

Pop quiz!

Why should you use the same data splits to compare each model?

Pop quiz!

Why should you use the same data splits to compare each model?

🍎 to 🍎

Pop quiz!

Does cross-validation measure just the accuracy of your model, or your entire workflow?

Pop quiz!

Does cross-validation measure just the accuracy of your model, or your entire workflow?

Your entire workflow

Other types of cross-validation

`vfold_cv()` - V Fold cross-validation

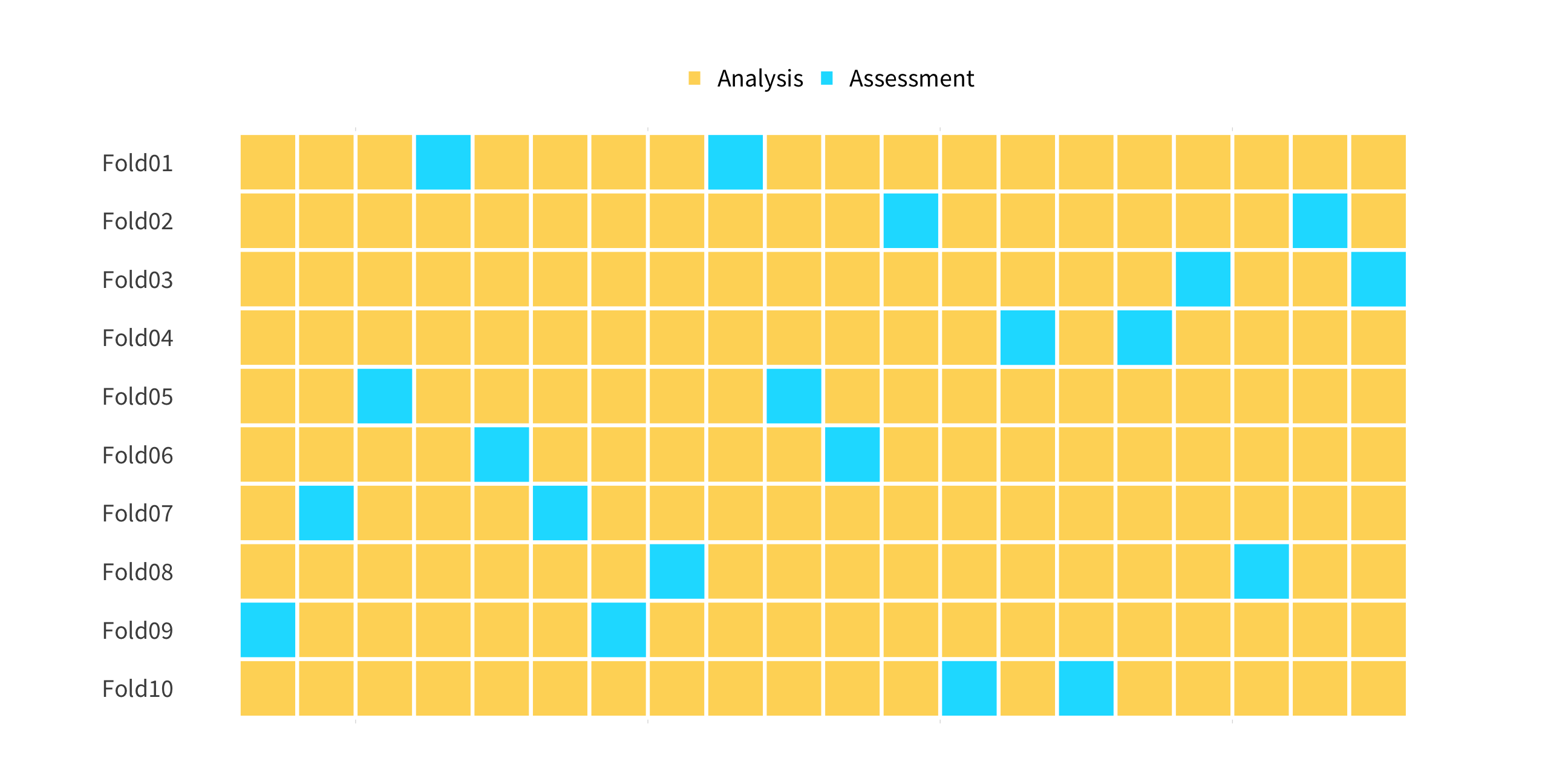
`loo_cv()` - Leave one out CV

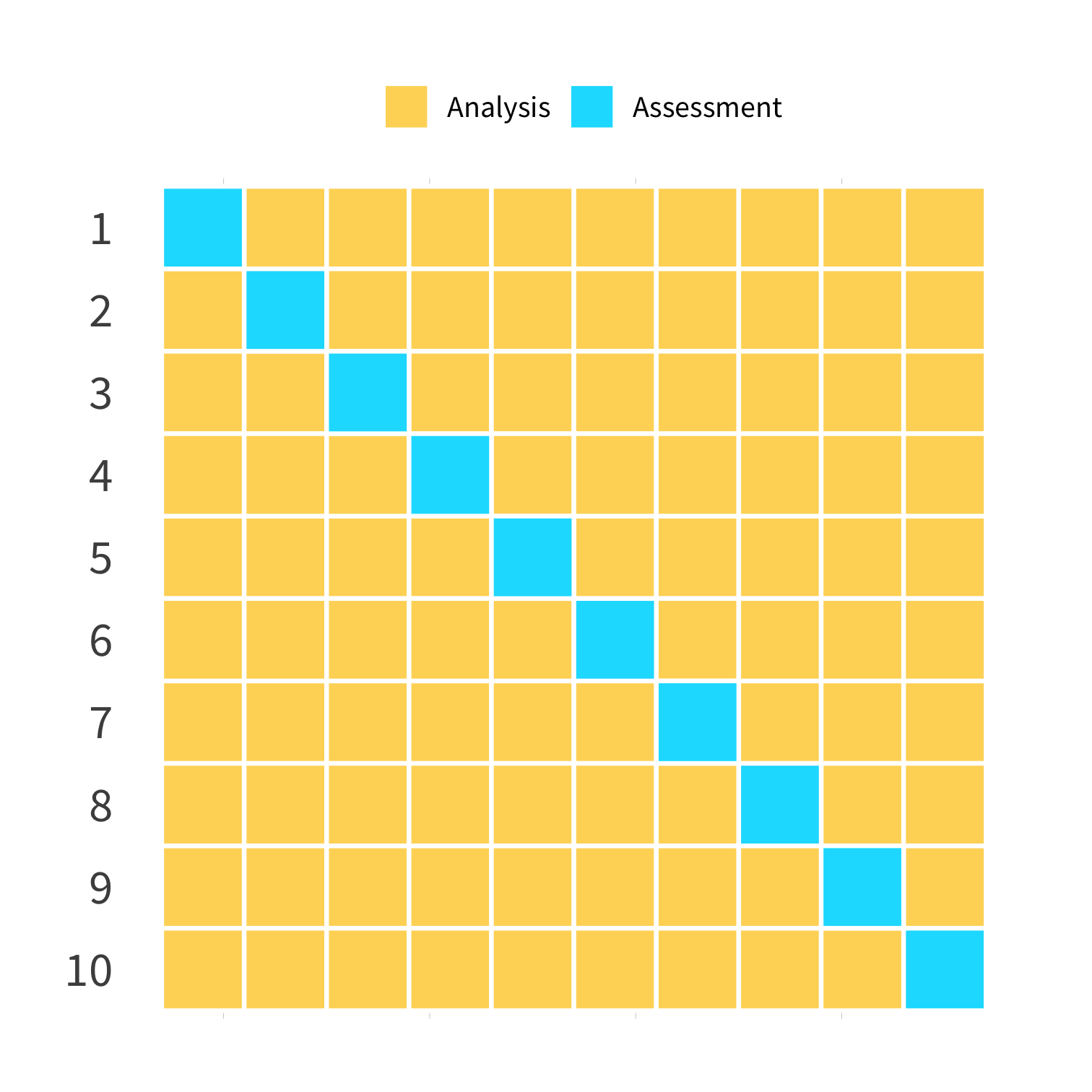
`mc_cv()` - Monte Carlo (random) CV

(Test sets sampled without replacement)

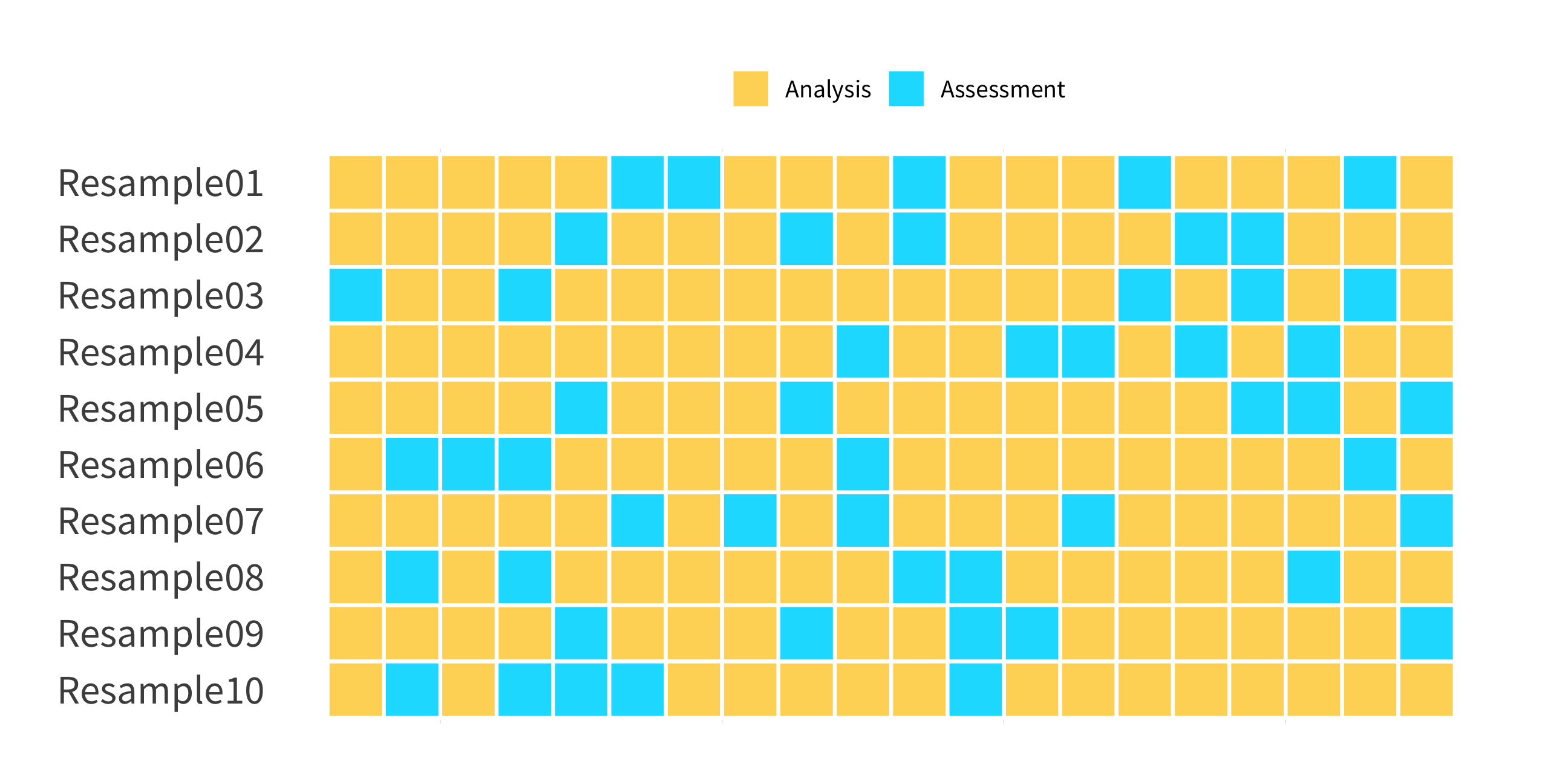
`bootstraps()`

(Test sets sampled with replacement)

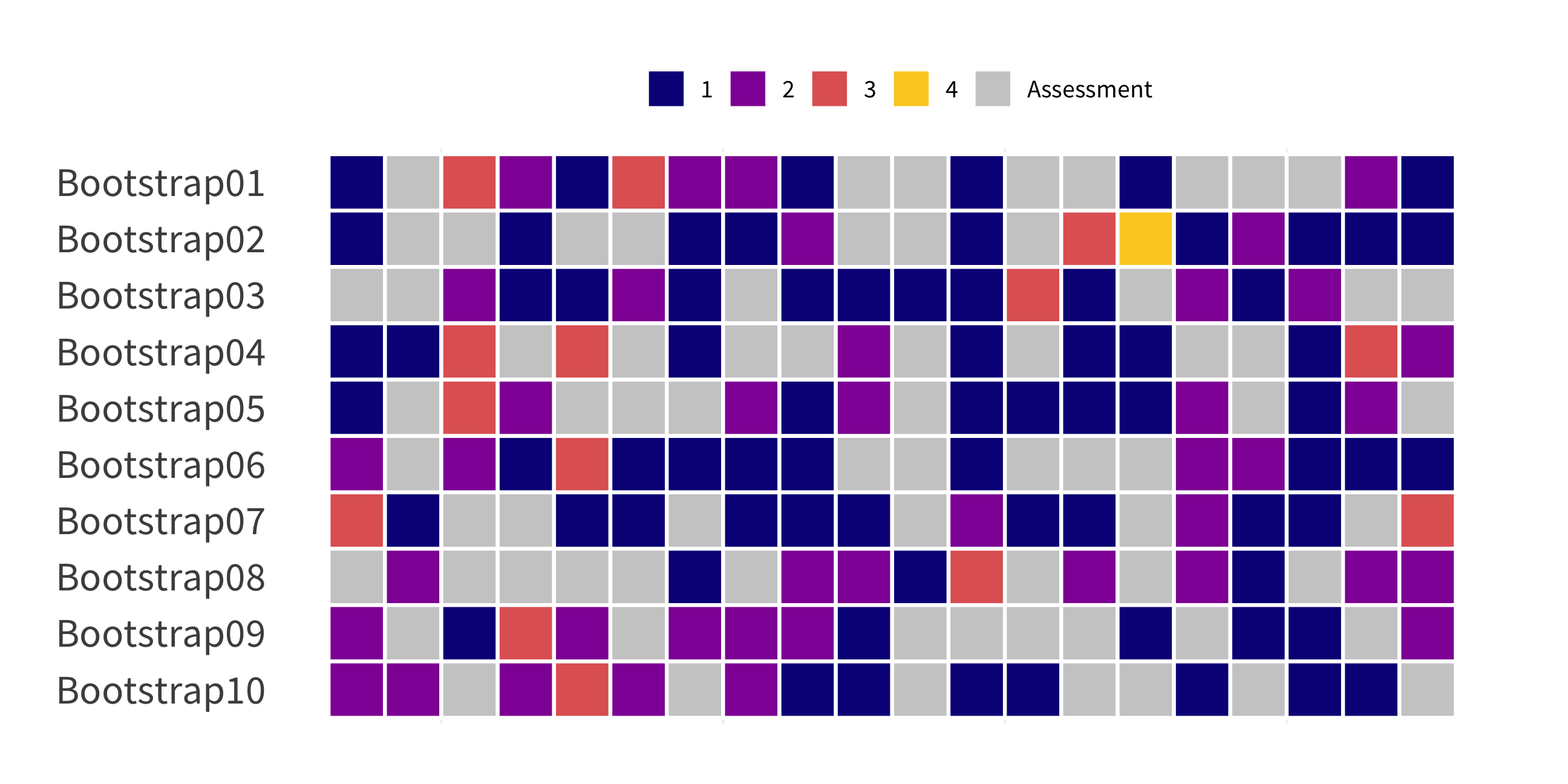
Resampling

Tidy Data Science with the Tidyverse and Tidymodels

W. Jake Thompson

https://tidyds-2021.wjakethompson.com · https://bit.ly/tidyds-2021

Tidy Data Science with the Tidyverse and Tidymodels is licensed under a Creative Commons Attribution 4.0 International License.

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help
s	Toggle scribble toolbox

Resampling

Tidy Data Science with the Tidyverse and Tidymodels

W. Jake Thompson

https://tidyds-2021.wjakethompson.com · https://bit.ly/tidyds-2021

Your Turn 0

Hypothesis

The Challenge

The Solution

The New Challenge

The good news

Palmer Penguins

bootstraps()

Your turn 1

Anatomy of a split

Anatomy of a split

Anatomy of a split

Anatomy of a split

Split data

Split data

analysis()

Split data

analysis()

assessment()

Pop quiz!

Correlation

Correlation

Your turn 2

Automation

(Applied) Data Science

map() and friends

map() and friends

Building our map()

Custom functions

Step 1: Create the code

Step 1: Create the code

Step 2: Wrap inside of function()

Step 2: Wrap inside of function()

Step 2: Wrap inside of function()

Step 3: Verify it works as expected

Step 3: Verify it works as expected

Building our map()

map() + mutate()

map_dbl() + mutate()

Your turn 3

Bootstrap summaries

Bootstrap summaries

Cross-validation

Your turn 4

Your turn 5

Pop quiz!

Consider

There has to be a better way...

V-fold cross-validation

Guess

Pop quiz!

Pop quiz!

Your turn 6

fit_resamples()

fit_resamples()

collect_metrics()

collect_metrics()

metric_set()

Your Turn 7

Comparing Models

Your Turn 8

Pop quiz!

Pop quiz!

Pop quiz!

Pop quiz!

Other types of cross-validation

vfold_cv() - V Fold cross-validation

loo_cv() - Leave one out CV

mc_cv() - Monte Carlo (random) CV

bootstraps()

Resampling

Tidy Data Science with the Tidyverse and Tidymodels

W. Jake Thompson

https://tidyds-2021.wjakethompson.com · https://bit.ly/tidyds-2021

Your Turn 0

Help

`bootstraps()`

`analysis()`

`analysis()`

`assessment()`

`map()` and friends

`map()` and friends

Building our `map()`

Step 2: Wrap inside of `function()`

Step 2: Wrap inside of `function()`

Step 2: Wrap inside of `function()`

Building our `map()`

`map()` + `mutate()`

`map_dbl()` + `mutate()`

`fit_resamples()`

`fit_resamples()`

`collect_metrics()`

`collect_metrics()`

`metric_set()`

`vfold_cv()` - V Fold cross-validation

`loo_cv()` - Leave one out CV

`mc_cv()` - Monte Carlo (random) CV

`bootstraps()`